Questões de Estatística do ano 2008

A partir dessas informações, julgue os itens seguintes.

O percentual da variação total de X₃ em relação a X₁ é superior a 20%.

• C. Certo
• E. Errado

Uma amostra aleatória simples X1, X2, ..., X16 será retirada de uma população normal com média 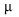e desvio-padrão 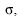, ambos desconhecidos. Para estimá-los, são propostas as estatísticas 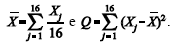. Com base nessas informações, julgue os itens seguintes.

Para a estimação da média populacional 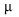, a média amostral é um estimador não tendencioso de mínima variância. Qualquer outro estimador não tendencioso para a estimação de 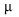, como, por exemplo, a mediana amostral, terá um desvio-padrão uniformemente maior que 0,25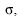

• C. Certo
• E. Errado

Uma amostra aleatória simples X1, X2, ..., X16 será retirada de uma população normal com média 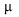e desvio-padrão 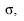, ambos desconhecidos. Para estimá-los, são propostas as estatísticas 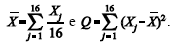. Com base nessas informações, julgue os itens seguintes.

A matriz de covariância do vetor aleatório 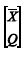 é a matriz de informação de Fisher.

• C. Certo
• E. Errado

Considere-se um vetor aleatório transposto xt = (X1, X2, X3) distribuído segundo uma distribuição normal com vetor de médias igual a 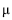t = (– 5, 0, 5) e matriz de covariância 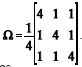. Com base nessas informações, julgue os itens subseqüentes.

A forma quadrática 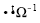é superior a 50 e inferior a 100.

• C. Certo
• E. Errado

Considere-se um vetor aleatório transposto xt = (X1, X2, X3) distribuído segundo uma distribuição normal com vetor de médias igual a 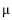t = (– 5, 0, 5) e matriz de covariância 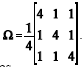. Com base nessas informações, julgue os itens subseqüentes.

Considerando os vetores transpostos v1 t = (– 5, 0, 0) e v2 t = (0, 0, 0), o quadrado da distância de Mahalanobis entre ambos é superior a 30 e inferior a 60.

• C. Certo
• E. Errado

Considere-se um vetor aleatório transposto xt = (X1, X2, X3) distribuído segundo uma distribuição normal com vetor de médias igual a 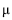t = (– 5, 0, 5) e matriz de covariância 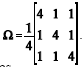. Com base nessas informações, julgue os itens subseqüentes.

• C. Certo
• E. Errado

Considere-se um vetor aleatório transposto xt = (X1, X2, X3) distribuído segundo uma distribuição normal com vetor de médias igual a 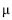t = (– 5, 0, 5) e matriz de covariância 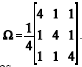. Com base nessas informações, julgue os itens subseqüentes.

Considere a matriz aleatória Y = [y1, y2], em que y1 e y2 são vetores aleatórios independentes e com a mesma distribuição de x - 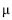. Nessa situação, YYt segue uma distribuição de Wishart com 2 graus de liberdade.

• C. Certo
• E. Errado

Considere que X seja uma variável aleatória uniformemente distribuída no intervalo [0, 1]. Se X $ 0,6, então Y = 1. Se X < 0,6, então Y = 0. Um programa de computador gerou a seguinte seqüência de realizações independentes de X: 0,09 0,56 0,37 0,48 0,90. Considerando essas informações, julgue os itens subseqüentes.

As quantidades padronizadas 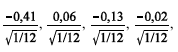 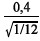são realizações de uma distribuição normal com média zero e variância 1.

• C. Certo
• E. Errado

Julgue os itens seguintes acerca da distribuição normal.

Considere duas variáveis aleatórias X e Y, cada uma distribuída segundo uma distribuição normal. A primeira possui média 5 e desvio padrão 5, e a segunda tem média 3 e desvio padrão 2. Nessa situação, a soma X + Y segue uma distribuição normal com média 8 e desvio padrão igual a 7.

• C. Certo
• E. Errado

Julgue os itens seguintes acerca da distribuição normal.

Se W segue uma distribuição normal com média 3 e variância 1, então P(W > 4 ) = P(W < 2).

• C. Certo
• E. Errado