Questões de Estatística do ano 2008

A partir dessas informações, julgue os itens seguintes.

A média 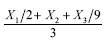 segue uma distribuição normal padrão.

• C. Certo
• E. Errado

Considere que X(t) represente o número de postos de trabalho disponíveis no instante t e que Y(t) represente o número de trabalhadores disponíveis no instante t para a ocupação desses postos. Considere também que X(t) e Y(t) sejam independentes e sigam processos estocásticos de Poisson. Nesse modelo, os valores esperados de X(t) e Y(t) são, respectivamente, iguais a 5t e 6t, em que t é um número real não-negativo, e o excesso de trabalhadores em relação à quantidade de postos disponíveis é definido pela diferença D(t) = Y(t) - X(t). Com base nessas definições, julgue os itens a seguir.

A média do processo X(t) + Y(t) é igual a 11t.

• C. Certo
• E. Errado

Considere que um processo estocástico de Wiener seja representado por 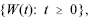 com Var[W(t)] = 0,25t e a transformação X(t) = [W(t)]². Nessa situação, julgue os itens que se seguem.

A covariância entre W(t) e W(t-4) é nula.

• C. Certo
• E. Errado

A partir das informações acima, julgue os itens subseqüentes.

A estimativa de razão para 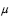 é inferior a R$ 13,00.

• C. Certo
• E. Errado

A partir das informações acima, julgue os itens subseqüentes.

A estimativa de razão para  é um estimador mais eficiente que a média aritmética.

• C. Certo
• E. Errado

A partir das informações acima, julgue os itens subseqüentes.

A estimativa de regressão linear para 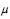 é superior a R$ 13,00.

• C. Certo
• E. Errado

Considere que Z seja uma variável aleatória normal padrão e que Y seja uma variável aleatória de Bernoulli com parâmetro p = 0,9. Considere também que a esperança condicional de Z para Y = 1 seja igual  a 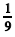 . Nessa situação, julgue os itens a seguir.

A esperança condicional do produto ZY dado que Y = 1 é igual a zero.

• C. Certo
• E. Errado

Considere que Z seja uma variável aleatória normal padrão e que Y seja uma variável aleatória de Bernoulli com parâmetro p = 0,9. Considere também que a esperança condicional de Z para Y = 1 seja igual  a 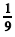 . Nessa situação, julgue os itens a seguir.

A covariância entre Z e Y é superior a 0,15.

• C. Certo
• E. Errado

Considerando um vetor aleatório (X, Y) distribuído na função de densidade conjunta 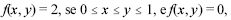caso contrário, julgue os itens a seguir.

A média de Y é inferior a 0,5.

• C. Certo
• E. Errado

Considere que X₁, X₂, ..., X_n seja uma amostra aleatória simples de uma distribuição X, cuja função de densidade é dada por para para x < 0 ou x > 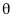 em que  > 0. Com base nessas informações, julgue os itens a seguir.

A média amostral 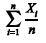 é o estimador de máxima verossimilhança para .

• C. Certo
• E. Errado