Questões de Estatística do ano 2008
Lista completa de Questões de Estatística do ano 2008 para resolução totalmente grátis. Selecione os assuntos no filtro de questões e comece a resolver exercícios.
Considerando uma variável aleatória X, uniformemente distribuída no intervalo [0, 12], julgue os itens a seguir.
P(X 2 < 1 ) < 0,1.
- C. Certo
- E. Errado
Considerando uma variável aleatória X, uniformemente distribuída no intervalo [0, 12], julgue os itens a seguir.

- C. Certo
- E. Errado
Em 2006, o rendimento do trabalhador com emprego formal somou R$ 43,5 bilhões, elevando o consumo e, conseqüentemente, a contratação de pessoal. Puxada pelo volume recorde de empregos formais e pela valorização dos rendimentos dos trabalhadores, a massa salarial registrou o maior crescimento desde 1995. De 2005 para 2006, a expansão chegou a 11,96%, atingindo o montante de R$ 43,5 bilhões. Esse aumento mostra que os brasileiros estão com mais dinheiro no bolso e, conseqüentemente, vão às compras. Para atender o ímpeto consumista, as empresas investem mais em produção, o que se reflete na contratação de novos trabalhadores. Tanto é que, em 2006, foram criados quase 1,917 milhão de empregos formais — o melhor resultado da série histórica da RAIS (relação anual de informações sociais), iniciada em 1985 —, um acréscimo de 5,77% em comparação a 2005. O setor de serviços foi o que mais contribuiu para a alta do emprego em 2006, com a abertura de 719,1 mil novas vagas. Em segundo lugar aparece a indústria de transformação (461,3 mil), seguida pelo comércio (325,2 mil) e administração pública (177,9 mil). A figura a seguir mostra alguns dados relevantes acerca da renda e da oportunidade de emprego do trabalhador brasileiro.
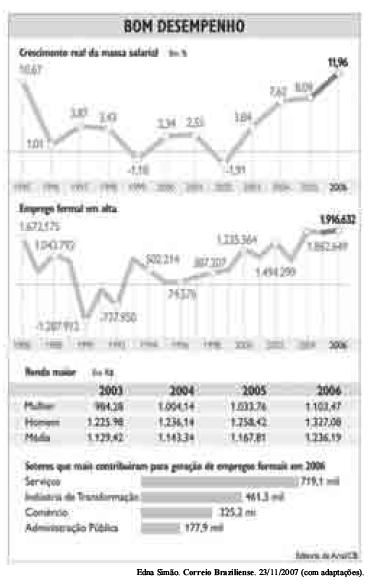
Considerando as informações ao lado, julgue os itens a seguir.
Em 2003, pela desigualdade de Markov, estima-se que a renda foi igual ou inferior a R$ 2.258,84 para metade dos trabalhadores com emprego formal.
- C. Certo
- E. Errado
Considere que, em um ambiente de trabalho industrial, as seguintes medições acerca da poluição do ar tenham sido observadas: 1, 6, 4, 3, 2, 3, 1, 5, 1, 4. Nessas situação, julgue os itens que se seguem.
Considere-se que os valores observados acerca da poluição do ar sejam realizações independentes de uma distribuição de Poisson com média constante. Nessa situação, pelo método da máxima verossimilhança, a probabilidade de se observar valores nulos na amostra é estimada igual a 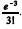
- C. Certo
- E. Errado
Considere que X(t) represente o número de postos de trabalho disponíveis no instante t e que Y(t) represente o número de trabalhadores disponíveis no instante t para a ocupação desses postos. Considere também que X(t) e Y(t) sejam independentes e sigam processos estocásticos de Poisson. Nesse modelo, os valores esperados de X(t) e Y(t) são, respectivamente, iguais a 5t e 6t, em que t é um número real não-negativo, e o excesso de trabalhadores em relação à quantidade de postos disponíveis é definido pela diferença D(t) = Y(t) - X(t). Com base nessas definições, julgue os itens a seguir.
Se Y(50) = 100, então Y(49) > 100.
- C. Certo
- E. Errado
Considere que Z seja uma variável aleatória normal padrão e que Y seja uma variável aleatória de Bernoulli com parâmetro p = 0,9. Considere também que a esperança condicional de Z para Y = 1 seja igual a 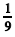 . Nessa situação, julgue os itens a seguir.
. Nessa situação, julgue os itens a seguir.
A esperança condicional de Z dado que Y = 0 é superior a 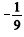
- C. Certo
- E. Errado
Considere uma amostra aleatória simples X1, X2, ..., Xn de uma distribuição com função de distribuição acumulada F(x), em que x é um número real. Para essa amostra, a função de distribuição acumulada empírica é definida como 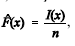 , em que I(x) é o número de elementos na amostra que são iguais ou inferiores a x. Com referência a essa situação, julgue os seguintes itens.
, em que I(x) é o número de elementos na amostra que são iguais ou inferiores a x. Com referência a essa situação, julgue os seguintes itens.
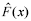 é um estimador não-viciado (ou não-tendencioso) para F(x).
é um estimador não-viciado (ou não-tendencioso) para F(x).
- C. Certo
- E. Errado
Considere uma amostra aleatória simples X1, X2, ..., Xn de uma distribuição com função de distribuição acumulada F(x), em que x é um número real. Para essa amostra, a função de distribuição acumulada empírica é definida como 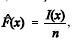 , em que I(x) é o número de elementos na amostra que são iguais ou inferiores a x. Com referência a essa situação, julgue os seguintes itens.
, em que I(x) é o número de elementos na amostra que são iguais ou inferiores a x. Com referência a essa situação, julgue os seguintes itens.
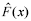 é um estimador consistente para F(x).
é um estimador consistente para F(x).
- C. Certo
- E. Errado
Considere uma amostra aleatória simples X1, X2, ..., Xn de uma distribuição com função de distribuição acumulada F(x), em que x é um número real. Para essa amostra, a função de distribuição acumulada empírica é definida como 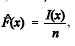 , em que I(x) é o número de elementos na amostra que são iguais ou inferiores a x. Com referência a essa situação, julgue os seguintes itens.
, em que I(x) é o número de elementos na amostra que são iguais ou inferiores a x. Com referência a essa situação, julgue os seguintes itens.
Para cada valor real x, a distribuição amostral de é 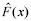 assintoticamente normal.
assintoticamente normal.
- C. Certo
- E. Errado
Considere uma amostra aleatória simples X1, X2, ..., Xn de uma distribuição com função de distribuição acumulada F(x), em que x é um número real. Para essa amostra, a função de distribuição acumulada empírica é definida como 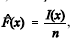 , em que I(x) é o número de elementos na amostra que são iguais ou inferiores a x. Com referência a essa situação, julgue os seguintes itens.
, em que I(x) é o número de elementos na amostra que são iguais ou inferiores a x. Com referência a essa situação, julgue os seguintes itens.
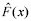 é um estimador de máxima verossimilhança para F(x).
é um estimador de máxima verossimilhança para F(x).
- C. Certo
- E. Errado


