Questões de Estatística do ano 2008

O número de pacientes (X) recebidos em um hospital para o atendimento ambulatorial e o número (Y) de pacientes recebidos no mesmo hospital para o atendimento de emergência seguem processos de Poisson homogêneos com médias, respectivamente, iguais a 10 pacientes/dia e 5 pacientes/dia. As variáveis aleatórias X e Y são independentes. Em média, 5% dos pacientes do atendimento ambulatorial são internados, enquanto 80% dos pacientes do atendimento emergencial são internados. Considerando que a decisão pela internação ou não internação seja feita no instante que o paciente chega ao hospital e que Z representa o número diário de pacientes internados nesse hospital, julgue os seguintes itens.

Considerando-se que cada dia possui 24 horas, o tempo médio de chegada entre dois pacientes consecutivos para o atendimento ambulatorial é inferior a 2 horas.

• C. Certo
• E. Errado

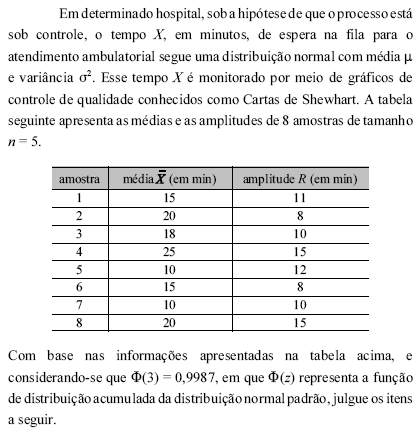
Considere que os limites de controle para a carta 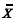 são construídos de modo que a probabilidade de que um ponto caia além desses limites, mesmo que o processo esteja sob controle, seja igual a 0,005. Nesse caso, o ARL 0 (average run length de um processo sob controle) será inferior a 350.

• C. Certo
• E. Errado

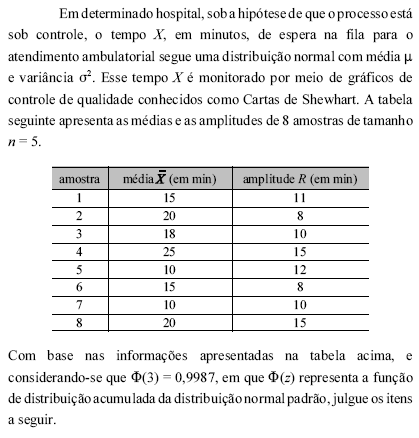
Considere que a probabilidade de se detectar uma mudança na média do processo seja igual a 0,25. Nessa situação, o número esperado de amostras até que a mudança seja detectada é inferior a 2.

• C. Certo
• E. Errado

Considere que X seja uma variável aleatória com função de densidade de probabilidade dada por f(x) = 3x ² , se -1 < x < 0, e f(x) = 0, se x < -1 ou x > 0, que Y seja uma variável aleatória com função de densidade de probabilidade dada por f(y) = 3y 2 , se 0 < y < 1, e f(y) = 0, se y < 0 ou y > 1 e que as variáveis X e Y sejam dependentes. Com base nessas informações, julgue os itens subseqüentes.

A covariância entre X e Y é inferior a 0,04 e é superior a -0,04.

• C. Certo
• E. Errado

Considere que X seja uma variável aleatória com função de densidade de probabilidade dada por f(x) = 3x ² , se -1 < x < 0, e f(x) = 0, se x < -1 ou x > 0, que Y seja uma variável aleatória com função de densidade de probabilidade dada por f(y) = 3y 2 , se 0 < y < 1, e f(y) = 0, se y < 0 ou y > 1 e que as variáveis X e Y sejam dependentes. Com base nessas informações, julgue os itens subseqüentes.

P(X < - 0,5) + P(Y < 0,5) = 1.

• C. Certo
• E. Errado

Considere que X seja uma variável aleatória com função de densidade de probabilidade dada por f(x) = 3x ² , se -1 < x < 0, e f(x) = 0, se x < -1 ou x > 0, que Y seja uma variável aleatória com função de densidade de probabilidade dada por f(y) = 3y 2 , se 0 < y < 1, e f(y) = 0, se y < 0 ou y > 1 e que as variáveis X e Y sejam dependentes. Com base nessas informações, julgue os itens subseqüentes.

A variável transformada X ² está uniformemente distribuída no intervalo (0, 1).

• C. Certo
• E. Errado

Com base em amostragens históricas, aplicáveis a modelos de longo prazo que cobrem previsões em um horizonte temporal grande, os analistas inferem distribuições que possibilitam uma generalização maior sobre os dados. Em relação a variáveis aleatórias e distribuições de probabilidade, julgue os itens a seguir. A estimação se refere a inferências sobre os parâmetros de um modelo estocástico para os dados. A predição diz respeito a evidências não observadas.

• C. Certo
• E. Errado

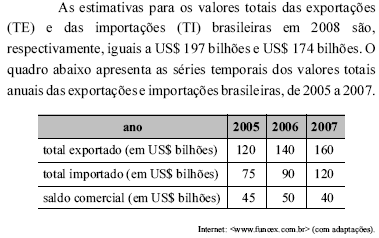
Com base nessas informações, julgue os itens subseqüentes.

Ajustando-se uma tendência linear do total importado (com intercepto não-nulo), em função do tempo, por regressão linear simples, a estimativa de mínimos quadrados do TI em 2008 será inferior a US$ 145 bilhões.

• C. Certo
• E. Errado

Considerando-se o modelo Y t = !a + b × (t ! 1978), os valores de a e b são, respectivamente, iguais a 33 e 0,5.

• C. Certo
• E. Errado

O erro-padrão da estimativa do coeficiente angular é superior a 0,4.

• C. Certo
• E. Errado