Questões de Estatística do ano 2008

A função de densidade conjunta de duas variáveis aleatórias contínuas, X e Y, é dada por:

• A.

  20%.

• B.

  30%.

• C.

  40%.

• D.

  50%.

• E.

  60%.

Avalie as afirmativas a seguir acerca de estatísticas suficientes minimais:

I. Uma estatística é suficiente minimal se é suficiente e se é uma função de alguma outra estatística suficiente.

II. Se um estimador de máxima verossimilhança é uma estatística suficiente então ele é uma estatística suficiente minimal.

III. Se um estimador de Bayes é uma estatística suficiente, então ele é uma estatística suficiente minimal.

Assinale:

• A.

  se somente a afirmativa II estiver correta.

• B.

  se somente as afirmativas I e II estiverem corretas.

• C.

  se somente as afirmativas I e III estiverem corretas.

• D.

  se somente as afirmativas II e III estiverem corretas.

• E.

  se todas as afirmativas estiverem corretas.

Considere que uma amostra aleatória simples de tamanho n = 5 de uma distribuição Bernoulli com probabilidade de sucesso p seja usada para testar H₀: p = 0,5 versus H₁: p = 0,7 e que seja usado o critério que rejeita a hipótese nula se forem observados 4 ou 5 sucessos. A probabilidade de se cometer erro tipo 1 é igual a:

• A.

  0,1875.

• B.

  0,15625.

• C.

  0,125.

• D.

  0,0625.

• E.

  0,03125.

Em um determinado município, 20% de todos os postos de gasolina testados quanto à qualidade do combustível apontaram o uso de combustíveis adulterados. Ao serem testados, 99% de todos os postos desse município que adulteraram combustível foram reprovados, mas 15% dos que não adulteraram também foram reprovados, ou seja, apresentaram um resultado falso-positivo. A probabilidade de um posto reprovado ter efetivamente adulterado o combustível é, aproximadamente,

• A.

  0,62

• B.

  0,50

• C.

  0,32

• D.

  0,20

• E.

  0,12

Um estudo para a estimação do número total, N, de usuários de drogas injetáveis foi realizado em um município no ano de 2006. A coleta de dados foi efetuada em duas fases por entrevistas face a face. A primeira fase (captura), que foi realizada nos meses de abril e maio de 2006, contou com n usuários entrevistados. A segunda fase (recaptura) foi realizada nos meses de agosto e setembro de 2006, com m usuários entrevistados. Com base nessas informações, considerando-se que N seja constante no período em questão e que todos os elementos da população tenham as mesmas chances de serem observados, julgue os itens subseqüentes.

Considerando-se que a amostragem na segunda fase seja aleatória simples sem reposição e que m = 2n, então a probabilidade de que metade da amostra seja formada por unidades recapturadas é igual a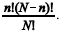

• C. Certo
• E. Errado

Mensalmente, Roberto compra um medicamento, podendo optar pelo genérico ou pelo não genérico. Considere que a opção é feita segundo um processo de Markov {X t }, em que t representa o mês 0, 1, 2, 3, ...., X t = 1 se Roberto adquire um medicamento genérico no mês t, e X t = 0 se Roberto adquire um medicamento não genérico no mês t. O elemento P ij da matriz P abaixo representa a probabilidade de transição do estado i no mês t para o estado j no mês t + 1, em que tanto i quanto j assumam os estados 0 ou 1.

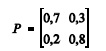
 Com base nas informações da situação hipotética acima, julgue os itens a seguir.

A probabilidade de transição do estado 0 no mês t para o estado 1 no mês t + 2 é inferior a 0,50.

• C. Certo
• E. Errado

Mensalmente, Roberto compra um medicamento, podendo optar pelo genérico ou pelo não genérico. Considere que a opção é feita segundo um processo de Markov {X t }, em que t representa o mês 0, 1, 2, 3, ...., X t = 1 se Roberto adquire um medicamento genérico no mês t, e X t = 0 se Roberto adquire um medicamento não genérico no mês t. O elemento P ij da matriz P abaixo representa a probabilidade de transição do estado i no mês t para o estado j no mês t + 1, em que tanto i quanto j assumam os estados 0 ou 1.

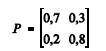
 Com base nas informações da situação hipotética acima, julgue os itens a seguir.

Dado que, nos meses t - 1 e t, Roberto fez a opção por medicamentos genéricos, a probabilidade de ele optar novamente pelo genérico no mês t + 1 é superior a 0,5.

• C. Certo
• E. Errado

Mensalmente, Roberto compra um medicamento, podendo optar pelo genérico ou pelo não genérico. Considere que a opção é feita segundo um processo de Markov {X t }, em que t representa o mês 0, 1, 2, 3, ...., X t = 1 se Roberto adquire um medicamento genérico no mês t, e X t = 0 se Roberto adquire um medicamento não genérico no mês t. O elemento P ij da matriz P abaixo representa a probabilidade de transição do estado i no mês t para o estado j no mês t + 1, em que tanto i quanto j assumam os estados 0 ou 1.

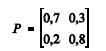
 Com base nas informações da situação hipotética acima, julgue os itens a seguir.

No limite estacionário, a probabilidade de Roberto adquirir um medicamento genérico é igual à probabilidade de Roberto adquirir um medicamento não genérico.

• C. Certo
• E. Errado

Mensalmente, Roberto compra um medicamento, podendo optar pelo genérico ou pelo não genérico. Considere que a opção é feita segundo um processo de Markov {X t }, em que t representa o mês 0, 1, 2, 3, ...., X t = 1 se Roberto adquire um medicamento genérico no mês t, e X t = 0 se Roberto adquire um medicamento não genérico no mês t. O elemento P ij da matriz P abaixo representa a probabilidade de transição do estado i no mês t para o estado j no mês t + 1, em que tanto i quanto j assumam os estados 0 ou 1.

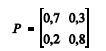
 Com base nas informações da situação hipotética acima, julgue os itens a seguir.

A cadeia é irredutível e aperiódica.

• C. Certo
• E. Errado

O número de pacientes (X) recebidos em um hospital para o atendimento ambulatorial e o número (Y) de pacientes recebidos no mesmo hospital para o atendimento de emergência seguem processos de Poisson homogêneos com médias, respectivamente, iguais a 10 pacientes/dia e 5 pacientes/dia. As variáveis aleatórias X e Y são independentes. Em média, 5% dos pacientes do atendimento ambulatorial são internados, enquanto 80% dos pacientes do atendimento emergencial são internados. Considerando que a decisão pela internação ou não internação seja feita no instante que o paciente chega ao hospital e que Z representa o número diário de pacientes internados nesse hospital, julgue os seguintes itens.

O número diário total de pacientes recebidos por esse hospital segue uma distribuição de Poisson com média e variância iguais a 15 e 225, respectivamente.

• C. Certo
• E. Errado