Questões de Estatística do ano 2009

Uma companhia necessita constituir provisões financeiras para despesas decorrentes de processos judiciais por reclamações trabalhistas. Considere que o total anual dessas despesas seja igual a X, em que X segue uma distribuição normal com média igual a R$ 30 mil e desvio padrão, R$ 10 mil. Tendo como referência essa situação, julgue os itens a seguir, assumindo que 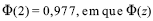 representa a função de distribuição acumulada da distribuição normal padrão.

Com 95,4% de confiança, é correto afirmar que, para o próximo ano, o total das despesas mencionadas está entre R$ 10 mil e R$ 50 mil.

• C. Certo
• E. Errado

Com base nessa situação hipotética, julgue os próximos itens.

A estimativa de máxima verossimilhança para a função geratriz de momentos de Y é igual a 0,2 + 0,8exp(t), em que t é um número real e exp(.) denota a função exponencial.

• C. Certo
• E. Errado

Com a correção de continuidade, a estimativa intervalar assintótica para a proporção r, com 99% de confiança, é 0,170 ± 0,078.

• C. Certo
• E. Errado

Considere um conjunto de variáveis aleatórias X₁, X₂, ..., X_n X_k X =1, em que cada variável X , k = 1, ..., n, representa o tempo gasto pelo k-ésimo oficial de justiça para o cumprimento de um mandado judicial. Essas variáveis aleatórias são independentes e identicamente distribuídas, segundo uma distribuição normal com média m e desvio padrão d, ambos desconhecidos. A partir dessas informações, julgue os itens de 69 a 76, considerando que 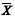 represente a média amostral desse conjunto de variáveis aleatórias.

A estatística 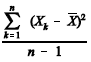é o estimador de máxima verossimilhança para d 2.

• C. Certo
• E. Errado

Considere um conjunto de variáveis aleatórias X₁, X₂, ..., X_n X_k X =1, em que cada variável X , k = 1, ..., n, representa o tempo gasto pelo k-ésimo oficial de justiça para o cumprimento de um mandado judicial. Essas variáveis aleatórias são independentes e identicamente distribuídas, segundo uma distribuição normal com média m e desvio padrão d, ambos desconhecidos. A partir dessas informações, julgue os itens de 69 a 76, considerando que 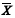 represente a média amostral desse conjunto de variáveis aleatórias.

A soma 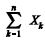é uma estatística suficiente e completa para a estimação dos parâmetros m e d.

• C. Certo
• E. Errado

A estimativa de máxima verossimilhança para o coeficiente b é superior a 0,5 e inferior a 0,7.

• C. Certo
• E. Errado

O estimador de máxima verossimilhança para 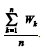 é .

• C. Certo
• E. Errado

Atenção: Para resolver às questões de números 56 e 57 use, dentre as informações dadas a seguir, as que julgar apropriadas. Se Z tem distribuição normal padrão, então:

P (Z > 1,64) = 0,05    P(Z > 2) = 0,02     P(0< Z < 1,75) = 0,46

Deseja-se estimar a proporção (p) de processos julgados por um tribunal regional do trabalho durante o período de 2000 até 2008. Uma amostra aleatória de 10.000 processos, selecionada da população (suposta infinita) de todos os processos, revelou que 5.000 foram julgados no referido período. Um intervalo de confiança, com coeficiente de confiança de 90% para p, baseado nessa amostra, é dado por

• A.

  0,5 ± 0,005

• B.

  0,5 ± 0,0062

• C.

  0,5 ± 0,0065

• D.

  0,5 ± 0,0082

• E.

  0,5 ± 0,01

Seja X uma variável aleatória representando a duração de vida de um equipamento. O desvio padrão populacional de X é igual a 20 horas. Uma amostra aleatória de 100 equipamentos forneceu uma duração de vida média igual a 1.000 horas obtendo-se um intervalo de confiança de 95% para a média populacional igual a [996,08 ; 1.003,92] (considerando a população normalmente distribuída e de tamanho infinito). Caso o tamanho da amostra tivesse sido de 400 e obtendo-se a mesma duração de vida média de 1.000 horas, o novo intervalo de confiança de 95% apresentaria uma amplitude de

• A.

  1,96 horas.

• B.

  2,94 horas.

• C.

  3,92 horas.

• D.

  5,88 horas.

• E.

  7,84 horas.

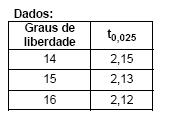
Os salários dos empregados de determinado ramo de atividade apresentam uma distribuição normal com uma variância populacional desconhecida. Uma amostra aleatória de 16 empregados deste ramo foi analisada apresentando uma média igual a R$ 1.500,00 e um desvio padrão igual a R$ 200,00. Considerando a população de tamanho infinito e t_0,025 o quantil da distribuição t de Student para teste unicaudal tal que P(t > t_0,025) = 0,025 com n graus de liberdade, obteve-se um intervalo de confiança de 95% para a média populacional. O intervalo obtido, com os valores em reais, foi igual a

• A.

  [1.473,50; 1.526,50]

• B.

  [1.473,00; 1.527,00]

• C.

  [1.394,00; 1.606,00]

• D.

  [1.393,50; 1.606,50]

• E.

  [1.392,50; 1.607,50]