Questões de Estatística do ano 2009

Por meio de convênios com um plano de saúde e com escolas de nível fundamental e médio, uma empresa oferece a seus 3.000 empregados a possibilidade de adesão. Sabe-se que 300 empregados aderiram aos dois convênios, 1.700 aderiram ao convênio com as escolas e 500 não aderiram a nenhum desses convênios.

Em relação a essa situação, julgue os itens seguintes de 38 a 40.

Escolhendo-se ao acaso um dos empregados dessa empresa, a probabilidade de ele ter aderido a algum dos convênios é igual a  .

• C. Certo
• E. Errado

Por meio de convênios com um plano de saúde e com escolas de nível fundamental e médio, uma empresa oferece a seus 3.000 empregados a possibilidade de adesão. Sabe-se que 300 empregados aderiram aos dois convênios, 1.700 aderiram ao convênio com as escolas e 500 não aderiram a nenhum desses convênios.

Em relação a essa situação, julgue os itens seguintes de 38 a 40.

A probabilidade de que um empregado escolhido ao acaso tenha aderido apenas ao convênio do plano de saúde é igual a .

• C. Certo
• E. Errado

Um estudo acerca do sucateamento de veículos automotores forneceu o modelo abaixo para a probabilidade condicional de certo tipo de veículo estar em condição de uso em função do seu tempo de uso X (em anos).

P(Y = 1|X = t) = exp(-0,4 )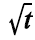

Nesse modelo, exp(.) representa a função exponencial; Y é uma variável aleatória binária que assume valor 1, se o veículo estiver em condição de uso, ou 0, se o veículo não estiver em condição de uso; t 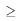 0 representa um instante (em anos) em particular; e a variável aleatória contínua X, é definida pela seguinte expressão.

P(X 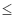 t) = 1 - exp(-0,5  )

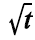 Com base nessas informações, julgue os itens que se seguem.

A probabilidade marginal P(Y = 1) é superior a 0,6.

• C. Certo
• E. Errado

Um estudo acerca do sucateamento de veículos automotores forneceu o modelo abaixo para a probabilidade condicional de certo tipo de veículo estar em condição de uso em função do seu tempo de uso X (em anos).

P(Y = 1|X = t) = exp(-0,4 )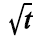

Nesse modelo, exp(.) representa a função exponencial; Y é uma variável aleatória binária que assume valor 1, se o veículo estiver em condição de uso, ou 0, se o veículo não estiver em condição de uso; t 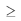 0 representa um instante (em anos) em particular; e a variável aleatória contínua X, é definida pela seguinte expressão.

P(X 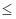 t) = 1 - exp(-0,5  )

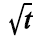 Com base nessas informações, julgue os itens que se seguem.

• C. Certo
• E. Errado

Considerando-se as informações acima, relativas a uma fila simples, baseada no processo de vida e morte, com taxas de chegada e de serviço constantes, com servidor único (s = 1), e em condição de estado de equilíbrio, julgue os itens de 89 a 93.

A probabilidade de que nenhum veículo esteja trafegando no trecho é igual a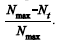

• C. Certo
• E. Errado

Considerando-se as informações acima, relativas a uma fila simples, baseada no processo de vida e morte, com taxas de chegada e de serviço constantes, com servidor único (s = 1), e em condição de estado de equilíbrio, julgue os itens de 89 a 93.

Considerando-se que o processo de chegada seja de Poisson, o intervalo médio de tempo entre chegadas de dois veículos consecutivos é igual a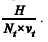

• C. Certo
• E. Errado

A distribuição dos tempos Y_i pertence à família exponencial.

• C. Certo
• E. Errado

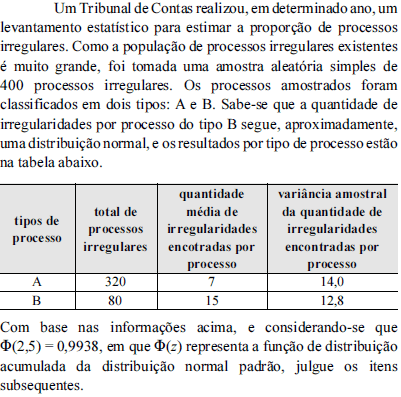
Se um processo do tipo B for selecionado ao acaso, considerando os resultados apresentados na tabela, estima-se que a probabilidade desse processo apresentar 47 ou mais irregularidades é superior a 0,01.

• C. Certo
• E. Errado

Considere que, em uma população, 80% dos indivíduos estejam satisfeitos com os serviços prestados por uma companhia aérea e que uma amostra aleatória simples de 10 pessoas seja retirada dessa população. Considere, ainda, que X represente o número de pessoas na amostra satisfeitas com os serviços prestados por essa companhia aérea, seguindo uma distribuição binomial. Com relação a essa situação hipotética e tomando 0,17 como valor aproximado de 0,8⁸ , julgue os itens subsequentes.

A probabilidade de se observarem exatamente 8 pessoas satisfeitas com os serviços prestados na amostra é superior a 0,5.

• C. Certo
• E. Errado

Considere duas variáveis aleatórias, V e Z, em que V possui distribuição binomial com n = 1 e p = 0,2, enquanto Z possui distribuição binomial com n = 1 e p = 0,8. Considerando que a covariância entre V e Z é igual a 0,04, julgue os itens que se seguem.

Não é possível ocorrer, simultaneamente, V = 1 e Z = 0.

• C. Certo
• E. Errado