Questões de Estatística do ano 2009

Seja uma tabela de contingência 2x2 na qual um fator corresponde à ocorrência ou não ocorrência de um evento. A técnica conhecida como razão das chances ou "odds ratio" pode ser aplicada para avaliar as chances de ocorrência do evento em relação ao seu complemento. Assim, suponha hipoteticamente que em determinado estado foi feito um estudo com ex-presidiários sobre a reincidência do delito de furto e a condição de trabalho. Os dados estão na tabela adiante.

Então, com base nos dados da tabela de contingência é correto afirmar que:

• A.

  Um ex-presidiário TI tem mais de 30% de chance, que o TCA, de voltar a furtar.

• B.

  Um ex-presidiário TCA tem exatamente 30% de chance de voltar a furtar.

• C.

  Um ex-presidiário TI tem menos de 20% de chance, que o TCA, de voltar a furtar.

• D.

  Um ex-presidiário TCA tem exatamente 20% de chance de voltar a furtar.

Seja o vetor aleatório os p pares de autovalores-autovetores de Considere as p componentes principais então

• A.

  

• B.

  

• C.

  

• D.

  

Considere então

• A.

  correl (X₁,X²) = correl(X₁,X₃) = -2/3; correl(X₂, X₃) = 0

• B.

  as variáveis aleatórias X₁, X₂ e X₃ são independentes

• C.

  pode-se afirmar que a função densidade conjunta de X₁, X₂ e X₃ é o produto das funções densidades marginais de X₁, X₂ e X₃

• D.

  V(X₁) = 9, V(X₂) = 4, V(X₃) = 4, Cov(X₁,X₂) + Cov(X₁,X₃) + Cov(X₂,X₃) = -16

Suponha que na rodovia BR116, em uma determinada Praça de Pedágio, a chegada dos veículos no intervalo de tempo (0, t] ocorre segundo um Processo de Poisson. Assim, as chegadas representadas pela variável aleatória Xt seguem uma distribuição de Poisson com parâmetro lt. Então, é correto afirmar que:

• A.

  A probabilidade de um número par de chegadas ocorrer é:

• B.

  A probabilidade de um número par de chegadas ocorrer é:

• C.

  A probabilidade de um número impar de chegadas ocorrer é:

• D.

  A probabilidade de um número impar de chegadas ocorrer é:

Seja um sistema em que se tem o Processo de Fila tipo M/M/1 no qual o número total de serviços requeridos é limitado por k N* devido à limitação do tamanho da fila. Considere que o sistema obedece a seguinte lei:

Então, é correto afirmar que considerando um "steady-state" a probabilidade de um pedido de serviço ser rejeitado e a probabilidade de que o sistema esteja completamente desocupado são respectivamente:

• A.

  

• B.

  

• C.

  

• D.

  

Considerando que, de acordo com Marshall, os fatores de risco podem ser compreendidos em termos de suas distribuições de probabilidade ao longo de um horizonte de tempo, com modelos muito diferentes sendo úteis conforme a situação seja de curto ou longo prazo, julgue os itens de 101 a 107, acerca de modelos e métodos analíticos.

A probabilidade de um sistema funcionar sem falhas durante um período de tempo (t) é dada pela soma contínua (integral) da probabilidade de falha p(t) ao longo de todo o tempo possível até o tempo t. O índice de falhas pode ser definido como o coeficiente da probabilidade de o evento ocorrer durante um período de tempo particular dividido pela confiabilidade do sistema nesse tempo.

• C. Certo
• E. Errado

O número de pessoas que chega ao guichê de uma repartição pública para autuação de processos apresenta uma distribuição de Poisson a uma taxa de duas pessoas por minuto. A probabilidade de que nos próximos 2 minutos chegue pelo menos uma pessoa neste guichê é

Observação: e = 2,71828...

• A.

  (e^{4 − 1}).e⁻⁴

• B.

  4.e⁻⁴

• C.

  (e^{4 − 4}).e⁻⁴

• D.

  2.[(e^{2 − 1}) ].e⁻²

• E.

  (e^{2 − 2}).e−²

Em um dado com seis faces numeradas de 1 a 6, a probabilidade de que cada um dos resultados ocorra é a mesma. Esse dado será lançado até que se obtenha o resultado 6. A probabilidade de que isso aconteça em, no máximo, 2 lançamentos é

• A.
• B.
• C.
• D.
• E.

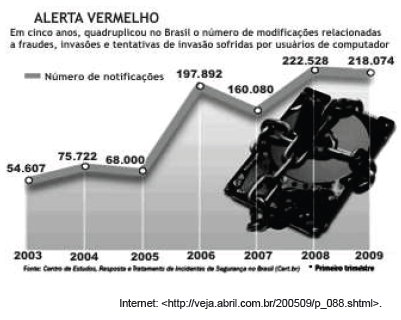
Tomando-se de forma aleatória uma das notificações mostradas no gráfico acima, a probabilidade de que ela tenha ocorrido em um ano ímpar é um número que está entre

• A.

  0,0 e 0,2.

• B.

  0,2 e 0,4.

• C.

  0,4 e 0,6.

• D.

  0,6 e 0,8.

• E.

  0,8 e 1,0.

A probabilidade de que, no lançamento de três dados comuns, honestos, a soma dos resultados seja igual a 18 é

• A.

  1/12

• B.

  1/36

• C.

  1/216

• D.

  3/18

• E.

  3/216