Questões de Estatística do ano 2009

Atenção: Para resolver às questões de números 38 e 39 considere o texto abaixo. Uma amostra com 80 pares de observações (X_i, Y_i), i = 1, 2, 3, . . . , 80; sendo as somas das observações de X_i e Y_i iguais a 560 e 2.400, respectivamente. Um estudo tinha como objetivo analisar a relação entre X e Y e adotou-se o modelo Y_i = α + βX_i + ε_i, em que i corresponde a i-ésima observação, α e β são parâmetros desconhecidos e εi o erro aleatório com as respectivas hipóteses consideradas para a regressão linear simples. Utilizou-se o método dos mínimos quadrados, com base na amostra, para o ajustamento do modelo obtendo-se para a estimativa de α o valor de 2.

Considerando a função linear obtida pelo método dos mínimos quadrados, tem-se que quando X varia de 1 unidade Y varia de

• A.

  2,0 unidades.

• B.

  2,5 unidades.

• C.

  3,0 unidades.

• D.

  3,5 unidades.

• E.

  4,0 unidades.

Atenção: Para resolver às questões de números 38 e 39 considere o texto abaixo. Uma amostra com 80 pares de observações (X_i, Y_i), i = 1, 2, 3, . . . , 80; sendo as somas das observações de X_i e Y_i iguais a 560 e 2.400, respectivamente. Um estudo tinha como objetivo analisar a relação entre X e Y e adotou-se o modelo Y_i = α + βX_i + ε_i, em que i corresponde a i-ésima observação, α e β são parâmetros desconhecidos e εi o erro aleatório com as respectivas hipóteses consideradas para a regressão linear simples. Utilizou-se o método dos mínimos quadrados, com base na amostra, para o ajustamento do modelo obtendo-se para a estimativa de α o valor de 2.

Se Y = f(X), em que f(X) é a função linear obtida pelo método dos mínimos quadrados, então a função Z, tal que Z = XY, atinge o valor mínimo quando X for igual a

• A.

  −0,75.

• B.

  −0,50.

• C.

  −0,25.

• D.

  0,00.

• E.

  0,25.

Instruções: Para responder às questões de 52 a 54 considere uma amostra aleatória de 10 pares de observações (Xi, Yi), i = 1, 2, 3, ..., 10 em que

 

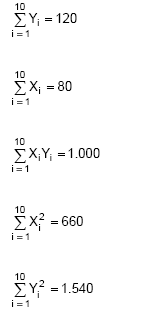
Obteve-se a partir do método dos mínimos quadrados o ajustamento do modelo Y1 = α + β X1 + εi em que α e β são parâmetros desconhecidos e εi o erro aleatório, com as respectivas hipóteses consideradas para a regressão linear simples.

Utilizando a equação da reta obtida pelo método dos mínimos quadrados, tem-se que o menor valor inteiro X tal que o valor estimado de Y seja superior a 10 é

• A.

  5

• B.

  6

• C.

  7

• D.

  8

• E.

  9

Instruções: Para responder às questões de 52 a 54 considere uma amostra aleatória de 10 pares de observações (Xi, Yi), i = 1, 2, 3, ..., 10 em que

 

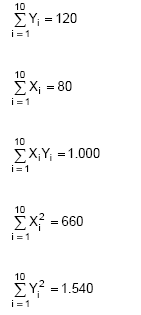
Obteve-se a partir do método dos mínimos quadrados o ajustamento do modelo Y1 = α + β X1 + εi em que α e β são parâmetros desconhecidos e εi o erro aleatório, com as respectivas hipóteses consideradas para a regressão linear simples.

O valor da estimativa S² da variância do modelo teórico, baseado nos dados fornecidos, é

• A.

  1,2500

• B.

  1,5625

• C.

  1,8750

• D.

  2,1250

• E.

  2,5000

Instruções: Para responder às questões de 52 a 54 considere uma amostra aleatória de 10 pares de observações (Xi, Yi), i = 1, 2, 3, ..., 10 em que

 

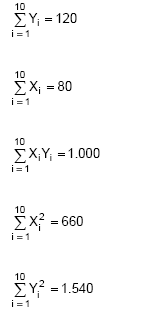
Obteve-se a partir do método dos mínimos quadrados o ajustamento do modelo Y1 = α + β X1 + εi em que α e β são parâmetros desconhecidos e εi o erro aleatório, com as respectivas hipóteses consideradas para a regressão linear simples.

Seja F_c o valor da estatística F (F calculado) utilizado para comparação com o F tabelado (variável F de Snedecor com m graus de liberdade no numerador e n graus de liberdade no denominador, ao nível de significância α) para testar a existência da regressão. Então,

• A.

  F_c = 80 e  = 8

• B.

  F_c = 32 e mn = 8

• C.

  F_c = 80 e (m + n) = 10

• D.

  F_c = 32 e (m + n) = 10

• E.

  F_c = 80 e (m + n) = 9

Considerando n pares (Xi; Yi) nos problemas de Regressão Linear Simples sabe-se que:

I. O modelo de regressão é dado por Yi = + ßXi +

II. A reta de regressão é dada por y' = a + bx

III. O erro aleatório é estimado pelo resíduo (yi - y'i )

 

Em relação as assertivas acima, pode-se afirmar que

• A.

  Todas são verdadeiras.

• B.

  Apenas II e III são verdadeiras.

• C.

  Apenas I e II são verdadeiras.

• D.

  Apenas I e III são verdadeiras.

Para ajustar uma curva a um conjunto de dados é usual utilizar o Método dos Mínimos Quadrados (MMQ). Sabe-se que:

I. O MMQ é uma técnica matemática de otimização que busca o melhor ajuste para um conjunto de dados.

II. O MMQ busca minimizar a soma dos erros quadráticos.

 

Considerando as assertivas acima, pode-se afirmar que:

• A.

  Somente a II é verdadeira.

• B.

  Ambas são falsas.

• C.

  Somente a I é verdadeira.

• D.

  Ambas são verdadeiras.

Para investigar a relação entre o tempo diário de ginástica laboral (T) e o nível de stress (S) foram observados 10 colaboradores. Foram obtidos os seguintes resultados:

I. O tempo de ginástica laboral variou no intervalo [2; 20] minutos e o nível de stress de [1; 50] pontos.

II. A reta de regressão ajustada foi s' = 60 – 2t com R²=0,81.

 

Em relação aos resultados acima, pode-se afirmar que:

• A.

  Para t= 25 minutos pode-se prever um nível de stress s'=10 pontos.

• B.

  Para um tempo médio de ginástica laboral de 11 minutos pode-se prever um nível de stress s'=34,20 pontos.

• C.

  Para cada minuto de ginástica laboral se espera um decréscimo de 2 pontos no nível de stress.

• D.

  O coeficiente de correlação é igual a r= 0,90.

Ainda com base no texto, julgue os itens seguintes.

• C. Certo
• E. Errado

Ainda com base no texto, julgue os itens seguintes.

O erro padrão da estimativa do coeficiente angular b é maior que 0,05.

• C. Certo
• E. Errado