Questões sobre Distribuição Normal

Instruções: Para responder às questões de números 32 a 34 utilize as informações a seguir.

A duração de vida de um aparelho elétrico tem distribuição normal com média 1.500 dias e terceiro quartil de 1.840 dias. Se esse tipo de aparelho tiver garantia de 300 dias, a porcentagem das vendas originais do aparelho que exigirá substituição é

• A.

  8%

• B.

  5%

• C.

  4%

• D.

  3%

• E.

  1%

Instruções: Para responder às questões de números 32 a 34 utilize as informações a seguir.

A experiência com trabalhadores de uma certa indústria indica que o tempo requerido para que um trabalhador, aleatoriamente selecionado, realize um serviço, é distribuído de maneira aproximadamente normal com desvio padrão de 12 minutos. Desejase, por meio de uma amostra aleatória, com reposição, estimar a média populacional. O tamanho desta amostra, para que a diferença em valor absoluto entre o verdadeiro valor populacional e sua estimativa seja de no máximo 2 minutos, com probabilidade de 96%, é

• A.

  64

• B.

  81

• C.

  100

• D.

  144

• E.

  196

Atenção: Para resolver às questões de números 56 e 57 use, dentre as informações dadas a seguir, as que julgar apropriadas. Se Z tem distribuição normal padrão, então:

P (Z > 1,64) = 0,05    P(Z > 2) = 0,02     P(0< Z < 1,75) = 0,46

A distribuição dos salários, em número de salários mínimos, dos funcionários do sexo masculino de uma empresa é uma variável aleatória X : N (5; 1) e a dos funcionários do sexo feminino é uma variável aleatória Y : N (5; 1,25). Sorteiam-se duas amostras aleatórias simples, independentes, de cada uma dessas distribuições, as duas com n elementos cada. Seja D = X − Y. O valor de n para que P (|D| ≤ 0,3) = 0,96, é

• A.

  36

• B.

  49

• C.

  64

• D.

  77

• E.

  100

• A.

  I e II.

• B.

  I, III e IV.

• C.

  II e III.

• D.

  III.

• E.

  I, II e III.

Atenção: Para resolver às questões de números 58 a 60 use, dentre as informações dadas a seguir, as que julgar apropriadas.

Se Z tem distribuição normal padrão, então:

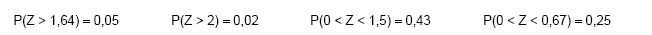
Seja X uma variável aleatória com distribuição normal com média 100 e desvio padrão 20. Se 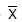 é a variável aleatória média amostral, tomada de uma amostra aleatória com reposição de n elementos da distribuição de X. O valor de n para que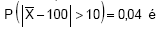

• A.

  16.

• B.

  25.

• C.

  36.

• D.

  49.

• E.

  64.

Atenção: Para resolver às questões de números 58 a 60 use, dentre as informações dadas a seguir, as que julgar apropriadas.

Se Z tem distribuição normal padrão, então:

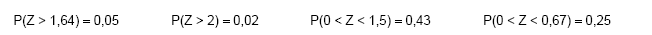
Os salários dos analistas de um tribunal é uma variável aleatória X, com distribuição normal com média μ e desvio padrão R$ 500,00. Sabendo que P(X < 5.000 reais) = 0,02, o valor do primeiro quartil de X, em reais, é

• A.

  5.755.

• B.

  5.665.

• C.

  5.605.

• D.

  5.500.

• E.

  5.410.

Atenção: Para resolver às questões de números 58 a 60 use, dentre as informações dadas a seguir, as que julgar apropriadas.

Se Z tem distribuição normal padrão, então:

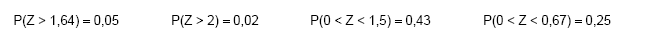
Um elevador tem seu funcionamento bloqueado se sua carga for superior a 310 kg.

Seja: X_i, é a variável aleatória que representa o peso do usuário i desse elevador, i = 1,2,...,n.

Sabendo-se que todas as X_i (i = 1,2,...,n.) têm distribuição normal com média 70 kg e desvio padrão 10 kg e são independentes, a probabilidade de ocorrer bloqueio numa tentativa de se transportar 4 passageiros é

• A.

  0,02.

• B.

  0,05.

• C.

  0,07.

• D.

  0.10.

• E.

  0,12.

Seja (X1, X2, X3) uma amostra aleatória simples de uma distribuição normal com média μ. Foram obtidos 3 estimadores para μ:

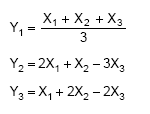
Então, APENAS

• A.

  Y₁ é não viesado.

• B.

  Y₁ e Y₃ são não viesados.

• C.

  Y₁ e Y₃ são viesados.

• D.

  Y₁ e Y₃ são viesados.

• E.

  Y₂ e Y₃ são viesados.

Instruções: Para resolver às questões de números 59 e 60, utilize dentre as informações dadas a seguir, as que julgar necessárias. Se Z tem distribuição normal padrão, então:

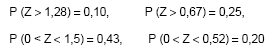
Sabe-se que, num município, impostos sobre imóveis , X, pagos por contribuintes, têm distribuição Normal com média μ e desvio padrão σ. Sabe-se que 30% dos impostos pagos são inferiores a R$ 1.200,00 e que 10% são superiores a R$ 3.000,00. O valor de μ e o valor do terceiro quartil da variável X, são dados, em reais, respectivamente, por

• A.

  1.670 e 2.300

• B.

  1.680 e 2.390

• C.

  1.700 e 2.420

• D.

  1.720 e 2.400

• E.

  1.720 e 2.390

Instruções: Para resolver às questões de números 59 e 60, utilize dentre as informações dadas a seguir, as que julgar necessárias. Se Z tem distribuição normal padrão, então:

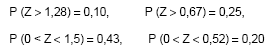
O custo de um produto é uma variável aleatória X com distribuição normal e sabe-se que este custo é a soma de três outros seguintes custos:

− custos fixos, que têm distribuição normal com média R$ 100,00 e desvio padrão R$ 20,00;

− custo da mão de obra, que tem distribuição normal com média R$ 500,00 e desvio padrão R$ 10,00;

− custo da matéria-prima, que é o dobro do custo da mão de obra.

Supondo que esses três custos sejam independentes, a probabilidade de X ser inferior a R$ 1.645,00 é

• A.

  0,93

• B.

  0,87

• C.

  0,85

• D.

  0,72

• E.

  0,64