Questões sobre Estimação e Intervalo de Confiança

• A.

  597,2 e 10.

• B.

  597 e 11.

• C.

  598,5 e 10.

• D.

  596,5 e 10.

• E.

  597 e 12,8.

Uma população X tem uma função densidade dada por , (0 x )

f(x) < < λ

= . Por meio de uma amostra aleatória de 10 elementos

• A.

  3.

• B.

  15/4

• C.

  27.

• D.

  6.

• E.

  27/4

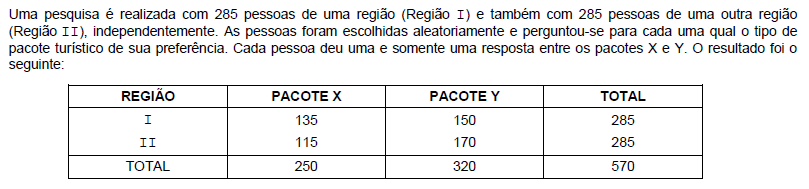
Utilizando o teste qui-quadrado a um nível de significância de 10%, observou-se que o valor crítico da distribuição qui-quadrado com 1 grau de liberdade é inferior ao valor do qui-quadrado observado. O valor do qui-quadrado observado e a conclusão da preferência com relação às regiões, a um nível de significância de 10%, são, respectivamente,

• A.

  2,600 ; depende da região.

• B.

  2,850 ; independe da região.

• C.

  2,850 ; depende da região.

• D.

  2,725 ; independe da região.

• E.

  2,725 ; depende da região.

Um estudo aponta como resultado o grau de associação moderado, de valor 0,6, entre a variável A e a variável B, estabelecendo um nível de confiança de 95%. De acordo com essas informações, assinale a alternativa correta:

• A.

  A confiança em 95% implica uma probabilidade de 5 casos em 100 de haver erro amostral.

• B.

  Os intervalos de confiança dizem respeito ao ato de prever que uma quantidade de questionários será invalidada por mau preenchimento.

• C.

  No caso acima, p = 0,05, indicando que a hipótese nula deve ser aceita em 95% dos casos.

• D.

  O tratamento estatístico garante a interpretação dos dados, sem necessidade de teoria prévia, como demonstra o exemplo acima, no qual o valor 0,6 garante que A causa B em 60% dos casos.

• E.

  P = 0,05, ou seja, há 95% de chance de aceitação da hipótese nula e rejeição da hipótese de trabalho, o que, por si só, invalida o resultado do grau de associação.

As lâmpadas fabricadas por A têm durabilidade média de 1.400 horas com desvio padrão de 200 horas; as do fabricante B têm durabilidade média de 1.200 horas com desvio padrão de 100 horas. Considerando a retirada de uma amostra aleatória simples de 125 lâmpadas de cada um dos fabricantes A e B, julgue os itens a seguir.

É praticamente impossível que a durabilidade média amostral das lâmpadas do fabricante B seja superior à durabilidade média amostral das lâmpadas produzidas pelo fabricante A.

• C. Certo
• E. Errado

Uma tabela de frequências absolutas refere-se à distribuição dos 80 preços unitários de venda de uma determinada peça no mercado. Analisando esta tabela, observam-se as seguintes informações:

I. Os intervalos de classe, fechados à direita e abertos à esquerda, apresentam a mesma amplitude igual a R$ 0,40.

II. O valor da mediana, obtido por interpolação linear, pertence ao intervalo [3,20; 3,60) e é igual a R$ 3,35.

III. 30 preços unitários são iguais ou superiores a R$ 3,60.

A porcentagem de preços unitários inferiores a R$ 3,20 é igual a

• A.

  42,5%.

• B.

  45,0%.

• C.

  46,0%.

• D.

  46,5%.

• E.

  47,5%.

O intervalo de confiança [48,975; 51,025], com um nível de confiança de 96%, corresponde a um intervalo para a média μ' de uma população normalmente distribuída, tamanho infinito e variância populacional igual a 16. Este intervalo foi obtido com base em uma amostra aleatória de tamanho 64. Deseja-se obter um intervalo de confiança de 96% para a média μ'’ de uma outra população normalmente distribuída, tamanho infinito e variância populacional igual a 64. Uma amostra aleatória desta população de tamanho 400 fornecerá um intervalo de confiança com amplitude igual a

• A.

  0,82.

• B.

  1,64.

• C.

  3,28.

• D.

  3,60.

• E.

  4,10.

• C. Certo
• E. Errado

Uma fábrica produz parafusos de índices C_p = 2,0 e C_pk = 0,5, que se referem aos diâmetros (em mm) desses parafusos. O controle do processo é do tipo 6 sigma, e sabe-se que o desvio padrão da distribuição dos diâmetros é igual a mm. Com base nessas 1/6 informações, julgue os itens a seguir, acerca de controle estatístico de qualidade.

Considere que, em uma amostra aleatória de parafusos, tenha se observado que a amplitude do intervalo de 95% de confiança foi igual a 2,5 mm. Nessa situação, é correto inferir que todos os parafusos produzidos possuíam diâmetros que atendiam às especificações do processo.

• C. Certo
• E. Errado

Uma empresa A pretende verificar a pressão máxima que um parafuso suporta sem entortar. Para isso, foi coletada uma amostra com 1000 parafusos, e foi verificado que em média um parafuso suporta 10,34kg e a variância da média é de 4kg². Considerando que o quantil 97,5% da distribuição Normal padrão é igual a 1,96, um intervalo de confiança de 95% para a média é dado por:

• A.

  (10,34-5,96; 10,34+5,96)

• B.

  (10,34-7,88; 10,34+7,88)

• C.

  (10,34-3,92; 10,34+3,92)

• D.

  (10,34-1,96; 10,34+1,96)

• E.

  (10,34-4; 10,34+4)