Questões sobre Estimação e Intervalo de Confiança

Dos 120 candidatos do sexo masculino que se submeteram a um concurso, 55 foram aprovados, enquanto dos 180 candidatos do sexo feminino que se submeteram ao mesmo concurso, 95 foram aprovados. Se desejarmos testar a hipótese estatística de que a proporção de aprovação no concurso independe do sexo dos candidatos, calcule o valor mais próximo da estatística do teste, que tem aproximadamente uma distribuição Qui quadrado com um grau de liberdade.

• A.

  1,91

• B.

  1,74

• C.

  1,65

• D.

  1,58

• E.

  1,39

Uma amostra aleatória de 100 funcionários de uma autarquia aponta que 25% dos funcionários consultados não são favoráveis á mudança da sede do clube para outra localidade. Qual deve ser tamanho da amostra, caso se queira com um nível de confiança de 95%, que a estimativa para a proporção populacional (verdadeira) de funcionários desfavoráveis a mudança, não defira em mais que 1%? Considere z = 2.

• A.

  570.

• B.

  75.

• C.

  750.

• D.

  7500.

Um engenheiro quer estimar o tempo médio de secagem de uma mistura de cimento usada para tapar buracos numa rodovia. O tempo médio, em minutos, de secagem observado para uma amostra aleatória de 36 buracos foi de 21 minutos, com uma variância de S² = 4. Qual o intervalo de confiança de 95% para o tempo médio de secagem dos buracos? Dados: t_29gl = 2,02 z_tab =1,96

• A.

  [20,89 ; 21,10].

• B.

  [20,32 ; 21,67].

• C.

  [20,34 ; 21,65].

• D.

  [19,93 ; 22,30].

Considerando que W seja um estimador pontual de um parâmetro 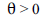 de uma distribuição D, julgue os itens a seguir.

Se W for obtido por máxima verossimilhança, então logW é o estimador de máxima verossimilhança de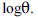

• C. Certo
• E. Errado

Uma população normal e de tamanho infinito apresenta uma média μ e variância populacional igual a 0,81. Pretende-se obter, a partir de uma amostra aleatória de tamanho 144 dessa população, um intervalo de confiança de 95% para μ. Considerando na distribuição normal padrão (Z) as probabilidades P(z > 1,96) = 0,025 e P(z > 1,64) = 0,05, o intervalo apresenta uma amplitude de

• A.

  0,246.

• B.

  0,264.

• C.

  0,294.

• D.

  1,764.

• E.

  3,528.

Uma amostra aleatória de 9 elementos foi extraída de uma população normal de tamanho infinito com média μ e variância desconhecida. O desvio padrão da amostra apresentou o valor de 1,25 e o intervalo de confiança de (1 − α) para μ: [14, 16] foi obtido com base nesta amostra. Sabe-se que para obtenção deste intervalo utilizou-se a distribuição t de Student com os correspondentes graus de liberdade, em que a probabilidade P (− T≤ t ≤ T) = (1 − α). Se T > 0, então o valor de T é

• A.

  2,4.

• B.

  2,7.

• C.

  3,0.

• D.

  3,6.

• E.

  4,2.

Os estimadores E' = mX₁ + (2m − 2n)X₂ + (2m − n) X₃ e E'' = (m − 2n) X₁ + (2m – 2n) X₂ + (4m − 2n) X₃ são 2 estimadores justos utilizados para a média μ de uma população normal. (X₁, X₂, X₃) corresponde a uma amostra aleatória de tamanho 3 desta população e m e n são parâmetros pertencentes aos números reais. O valor de (m + n) é igual a

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

• A.

  0,125.

• B.

  0,250.

• C.

  0,320.

• D.

  0,400.

• E.

  0,625.

Considere que os salários de todos os 530 empregados de uma empresa sejam normalmente distribuídos com uma média μ e um desvio padrão populacional igual a R$ 149,50. Uma amostra aleatória de 169 destes salários (sem reposição) apresentou uma média de X reais. Com base no resultado da amostra, deseja-se testar a hipótese, ao nível de significância de 5%, se μ é superior a R$ 2.000,00 sendo formuladas as hipóteses H_o: μ = R$ 2.000,00 (hipótese nula) e H₁: μ > R$ 2.000,00 (hipótese alternativa). Sabe-se que H_o não foi rejeitada considerando a informação da distribuição normal padrão (Z) que a probabilidade P (z > 1,64) = 0,05. O valor de X é, no máximo,

• A.

  R$ 2.037,72.

• B.

  R$ 2.031,16.

• C.

  R$ 2.018,86.

• D.

  R$ 2.015,58.

• E.

  R$ 2.007,79.

Seja uma variável aleatória X, em que uma amostra aleatória de 6 elementos {x₁, x₂, x₃, x₄, x₅, x₆} com x₁ < x₂ < x₃ < x₄ < x₅ < x₆, foi extraída da população. Considerando que [x₂, x₅] é um intervalo de confiança para a mediana de X, o nível de confiança deste intervalo é

• A.

  

• B.

  

• C.

  

• D.

  

• E.