Questões sobre Média

Suponha que ao realizar um experimento, o evento A ocorra com probabilidade p e não ocorra com probabilidade (1 − p). Sejam as variáveis aleatórias:

− X que representa a quantidade de repetições do experimento, consideradas independentes umas das outras, até que A ocorra pela primeira vez.

− Y que assume o valor 180 se X = 3 e o valor 90 se X ≠ 3.

Se o valor da variância de X é 6, o valor da média de Y é igual a

• A.

  4/27.

• B.

  230/3.

• C.

  310/3.

• D.

  56/27.

• E.

  230/3.

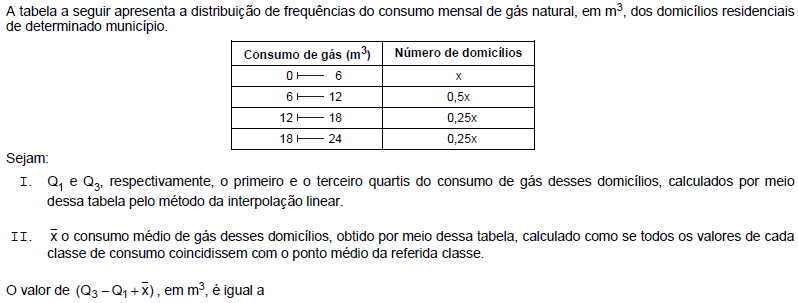
• A.

  15,25.

• B.

  12,50.

• C.

  12,75.

• D.

  10,75.

• E.

  17,25.

Segundo dados do site http://portalibre.fgv.br/main.jsp?lumChannelId=40288081 1D8E34B9011D92B6B6420E96, da FGV- Fundação Getúlio Vargas, acessado em 04/12/2010, o cálculo do índice Geral de Preços (IGP) é feito através da média aritmética ponderada de três outros índices de preços, quais sejam o índice de Preços ao Produtor Amplo (IPA), o Índice de Preços ao Consumidor (IPC) e o Índice Nacional de Custo da Construção (INCC). Os pesos de cada um dos índices componentes correspondem a parcelas da despesa interna bruta, calculadas com base nas Contas Nacionais – resultando na seguinte distribuição: peso 6 para o IPA, peso 3 para o IPC e peso 1 para o INCC. O IGP de novembro de 2010, sabendo que os índices registrados no mês foram IPA(1,49%), IPC(0,62%) e INCC(0,24%), foi de

• A.

  11,04%.

• B.

  12,35%

• C.

  2,35%.

• D.

  1,45%

• E.

  1,104%.

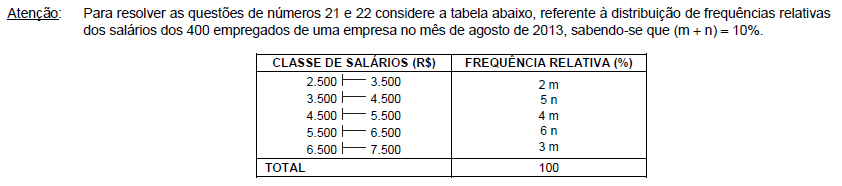O valor da média aritmética dos salários dos empregados foi obtido considerando-se que todos os valores incluídos num intervalo de classe são coincidentes com o ponto médio deste intervalo. O número de empregados correspondente ao intervalo de classe a que pertence o valor da média aritmética é igual a

• A. 80.
• B. 60.
• C. 40.
• D. 100.
• E. 120.

Em um órgão público, verifica-se que a média aritmética dos salários dos funcionários com nível superior supera a média aritmética dos restantes dos funcionários em R$ 2.000,00. Sabe-se que o desvio padrão dos salários dos funcionários com nível superior é igual a R$ 500,00 e dos restantes dos funcionários é igual a R$ 300,00, com os respectivos coeficientes de variação iguais. Se 40% dos funcionários possuem nível superior, então a média aritmética dos salários de todos os funcionários deste órgão público é igual a

• A. R$ 3.500,00.
• B. R$ 3.200,00.
• C. R$ 3.600,00.
• D. R$ 3.800,00.
• E. R$ 3.900,00.

Uma amostra aleatória de tamanho 100 foi extraída de uma população normalmente distribuída de tamanho infinito e com uma variância populacional igual a 25. Deseja-se verificar, ao nível de significância de 1%, se a média μ da população é inferior a 27 com a formulação das hipóteses H₀: μ = 27 (hipótese nula) e H₁: μ < 27 (hipótese alternativa). Considere na curva normal padrão (Z) a probabilidade P(Z > 2,33) = 0,01. O menor valor encontrado para a média amostral, tal que H₀ não seja rejeitada é

• A. 24,670.
• B. 25,835.
• C. 26,150.
• D. 27,865.
• E. 28,165.

Considere os seguintes cálculos para a média de n valores denotados por x₁, x₂, ... xn nos quais w₁, w₂, ... wn são constantes positivas.

As médias aritméticas simples, aritmética ponderada, geométrica e harmônica são calculadas, respectivamente, por

• A. I, II, III e IV.
• B. I, II, IV e III.
• C. I, III, II e IV.
• D. I, III, IV e II.
• E. I, IV, II e III.

A média geométrica dos números 4, 8 e 16 é

• A.

  maior que a respectiva média aritmética.

• B.

  inferior a 6.

• C.

  igual a 8.

• D.

  igual a 4.

• E.

  superior a 9.

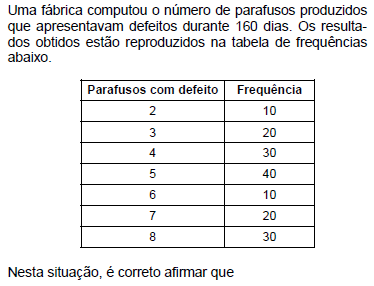
• A.

  a média aritmética dessa distribuição é menor que a mediana.

• B.

  multiplicando o número de parafusos com defeito por dois (2), o desvio padrão da nova distribuição também será multiplicado por dois (2) em relação à distribuição original.

• C.

  a moda dessa distribuição é superior à mediana.

• D.

  dividindo-se pela metade o número de parafusos com defeito, a variância da nova distribuição será dividida pela metade em relação à distribuição original.

• E.

  somando-se dois (2) às frequências da tabela, o desvio padrão e a variância da nova distribuição serão duas unidades maiores em relação aos da distribuição original.

É correto afirmar que, no teste de hipóteses para comparar duas médias populacionais,

• A. os erros tipo I e tipo II são eventos complementares.
• B. quanto maior o nível de significância, maior será o valor – p.
• C. o poder do teste aumenta com a redução do tamanho da amostra.
• D. quanto menor o tamanho da amostra, menor será o nível de significância.
• E. o poder do teste aumenta com o aumento da diferença entre as médias populacionais.