Questões sobre Mediana

Uma prefeitura registrou o aumento do valor venal V (em R$ por metro quadrado) de 200 imóveis localizados em certo bairro residencial, conforme apresentado na tabela a seguir.

 

Com base nessas informações, julgue os itens a seguir.

A mediana, que é igual a R$ 25,00/m², é o valor que divide os 50% valores mais baixos dos 50% mais altos.

• C. Certo
• E. Errado

Em uma unidade de atendimento ambulatorial, foi feito um estudo em um grupo de 18 pacientes para avaliação do conhecimento referente à aplicação de insulina. Foi utilizado um teste de 30 itens e foram computados escores para cada participante. Os resultados encontram-se na tabela a seguir.

 

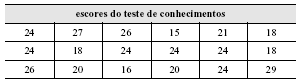
Com base na situação hipotética apresentada e considerando a estatística aplicada, julgue os itens subseqüentes.

A mediana dessa distribuição é igual a 15.

• C. Certo
• E. Errado

Determine a mediana do seguinte conjunto de dados: 58, 95, 17, 44, 63, 9, 57, 21, 88, 12, 31, 28, 73, 5 e 56.

• A.

  28.

• B.

  31.

• C.

  44.

• D.

  50.

• E.

  56.

Com base nessas informações e considerando que o valor 100 é representado nesses diagramas como 10|0, julgue os itens que se seguem.

A mediana da distribuição do número de livros destruídos pelas chuvas foi igual a 101.

• C. Certo
• E. Errado

Ordenados os elementos da amostra, x é o valor (pertencente ou não à amostra) que a divide ao meio, isto é, 50% dos elementos da amostra são menores ou iguais a x e os outros 50% são maiores ou iguais a x.

Para a sua determinação utiliza-se a seguinte regra, depois de ordenada a amostra de n elementos:

Se n é ímpar, x é o elemento médio.

Se n é par, x a semi-soma dos dois elementos médios.

Trata-se como regra geral:

• A.

  da média;

• B.

  da moda;

• C.

  da mediana;

• D.

  do desvio Padrão;

• E.

  do t de “Student”.

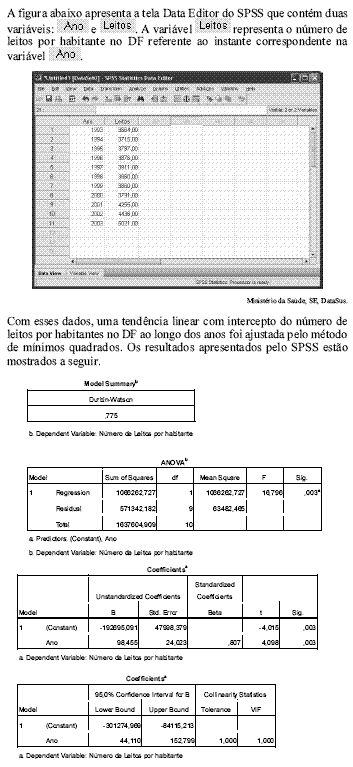
Tendo como referência essas informações, julgue os itens de 64 a 76.

A mediana do número de leitos hospitalares por habitante no DF foi superior a 3.900.

• C. Certo
• E. Errado

Considere que X seja uma variável aleatória com função de densidade de probabilidade dada por f(x) = 3x ² , se -1 < x < 0, e f(x) = 0, se x < -1 ou x > 0, que Y seja uma variável aleatória com função de densidade de probabilidade dada por f(y) = 3y 2 , se 0 < y < 1, e f(y) = 0, se y < 0 ou y > 1 e que as variáveis X e Y sejam dependentes. Com base nessas informações, julgue os itens subseqüentes.

A mediana de Y é inferior a 0,5.

• C. Certo
• E. Errado

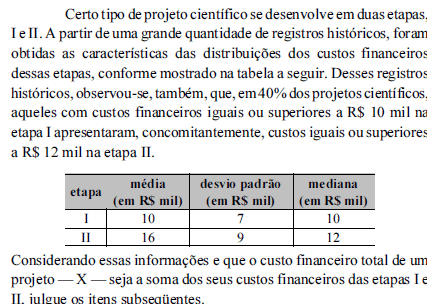
Em pelo menos 50% dos projetos científicos, os custos financeiros na etapa I foram iguais ou superiores a R$ 10 mil.

• C. Certo
• E. Errado

A tabela abaixo apresenta a distribuição do valor (em número de salários mínimos) do salário pago aos funcionários da fábrica Y no mês de maio de 2006. Calcule a média e a mediana do valor do salário pago pela fábrica Y no mês de maio de 2006.

• A.

  3,3 salários mínimos e 2,67 salários mínimos.

• B.

  3,3 salários mínimos e 3,3 salários mínimos.

• C.

  3,5 salários mínimos e 3,0 salários mínimos.

• D.

  3,8 salários mínimos e 2,67 salários mínimos.

• E.

  3,8 salários mínimos e 2,67 salários mínimos.

Considere o histograma da variável X.

O valor da mediana de X é

• A. 25,0
• B. 32,5
• C. 37,5
• D. 40,0
• E. 42,0