Questões sobre Regressão
Lista completa de Questões sobre Regressão para resolução totalmente grátis. Selecione os assuntos no filtro de questões e comece a resolver exercícios.
Um estudo sobre a segmentação do mercado de trabalho comparou o salário daquele que trabalha por conta própria (Y, em R$ mil) com o salário daquele que tem a carteira assinada (X, em R$ mil). Foi ajustado um modelo de regressão linear na forma Y = ax + b + g, em que a e b são os coeficientes do modelo e g representa um erro aleatório com média zero e desvio-padrão 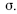 As estimativas de mínimos quadrados ordinários para os coeficientes a e b foram respectivamente iguais a 0,5 e R$ 6 mil. A quantidade de observações utilizadas para o ajuste do modelo foi igual a 400, e os desvios-padrão amostrais de Y e X foram, respectivamente, iguais a R$ 2 mil e R$ 1,5 mil.
As estimativas de mínimos quadrados ordinários para os coeficientes a e b foram respectivamente iguais a 0,5 e R$ 6 mil. A quantidade de observações utilizadas para o ajuste do modelo foi igual a 400, e os desvios-padrão amostrais de Y e X foram, respectivamente, iguais a R$ 2 mil e R$ 1,5 mil.
Com base nessas informações, julgue os itens subseqüentes.
A estimativa de 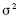 é superior a 3.
é superior a 3.
- C. Certo
- E. Errado
Um estudo sobre a segmentação do mercado de trabalho comparou o salário daquele que trabalha por conta própria (Y, em R$ mil) com o salário daquele que tem a carteira assinada (X, em R$ mil). Foi ajustado um modelo de regressão linear na forma Y = ax + b + g, em que a e b são os coeficientes do modelo e g representa um erro aleatório com média zero e desvio-padrão 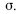 As estimativas de mínimos quadrados ordinários para os coeficientes a e b foram respectivamente iguais a 0,5 e R$ 6 mil. A quantidade de observações utilizadas para o ajuste do modelo foi igual a 400, e os desvios-padrão amostrais de Y e X foram, respectivamente, iguais a R$ 2 mil e R$ 1,5 mil.
As estimativas de mínimos quadrados ordinários para os coeficientes a e b foram respectivamente iguais a 0,5 e R$ 6 mil. A quantidade de observações utilizadas para o ajuste do modelo foi igual a 400, e os desvios-padrão amostrais de Y e X foram, respectivamente, iguais a R$ 2 mil e R$ 1,5 mil.
Com base nessas informações, julgue os itens subseqüentes.
Considere-se a situação em que seja feito um ajuste na forma
invertida 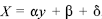
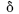 representa um erro
representa um erro aleatório com média zero e desvio-padrão constante, 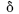
são os coeficientes do modelo. Nessa situação, o coeficiente
de determinação desse modelo é inferior a 15% e a
estimativa de mínimos quadrados para o coeficiente
" éigual a 2.
- C. Certo
- E. Errado
Um estudo sobre a segmentação do mercado de trabalho comparou o salário daquele que trabalha por conta própria (Y, em R$ mil) com o salário daquele que tem a carteira assinada (X, em R$ mil). Foi ajustado um modelo de regressão linear na forma Y = ax + b + g, em que a e b são os coeficientes do modelo e g representa um erro aleatório com média zero e desvio-padrão 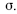 As estimativas de mínimos quadrados ordinários para os coeficientes a e b foram respectivamente iguais a 0,5 e R$ 6 mil. A quantidade de observações utilizadas para o ajuste do modelo foi igual a 400, e os desvios-padrão amostrais de Y e X foram, respectivamente, iguais a R$ 2 mil e R$ 1,5 mil.
As estimativas de mínimos quadrados ordinários para os coeficientes a e b foram respectivamente iguais a 0,5 e R$ 6 mil. A quantidade de observações utilizadas para o ajuste do modelo foi igual a 400, e os desvios-padrão amostrais de Y e X foram, respectivamente, iguais a R$ 2 mil e R$ 1,5 mil.
Com base nessas informações, julgue os itens subseqüentes.

- C. Certo
- E. Errado
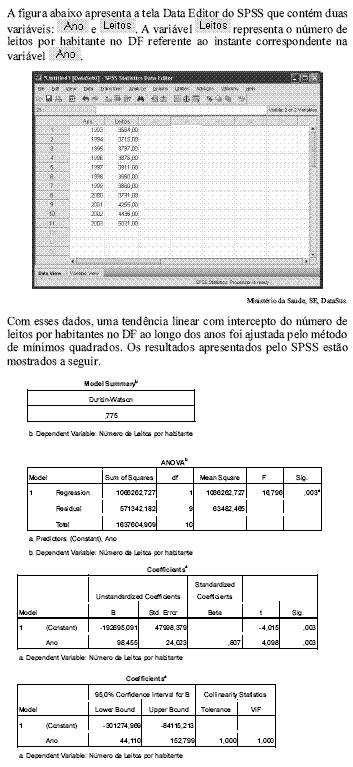
Tendo como referência essas informações, julgue os itens de 64 a 76.
O intervalo de confiança de 95% para o coeficiente angular da reta de regressão, sob a hipótese de normalidade dos erros aleatórios, é obtido com base em uma distribuição t de Student com 2 graus de liberdade.
- C. Certo
- E. Errado
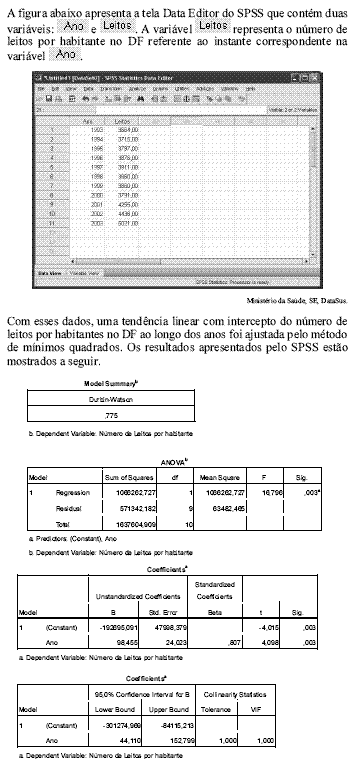
Tendo como referência essas informações, julgue os itens de 64 a 76.
A estimativa do desvio padrão residual é inferior a 300.
- C. Certo
- E. Errado
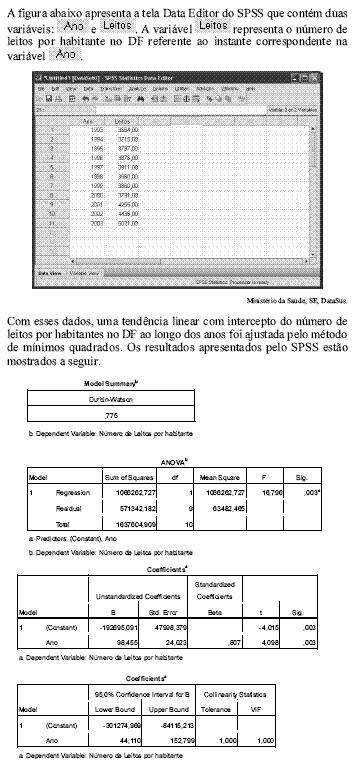
Tendo como referência essas informações, julgue os itens de 64 a 76.
O percentual da variação da variável  explicada pela tendência linear é superior a 60%.
explicada pela tendência linear é superior a 60%.
- C. Certo
- E. Errado
Na estimativa das regressões lineares múltiplas, o problema de multicolinearidade tende a ocorrer quando
- A.
duas variáveis independentes se correlacionam fortemente.
- B.
a variável dependente for correlacionada com alguma variável independente.
- C.
o coeficiente de determinação R2 for muito baixo.
- D.
os dados da regressão forem transversais.
- E.
houver variáveis independentes binárias.
O gráfico abaixo mostra os pares de observações de duas variáveis X e Y relacionadas pela regressão linear simples Y = a + bX + u, (onde a e b são coeficientes a serem estimados e u são os erros aleatórios).
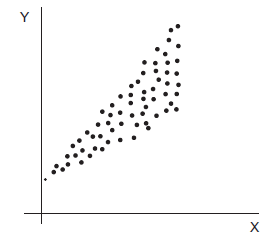
O exame do gráfico sugere que
- A.
Y e X não se relacionam.
- B.
a relação é não linear.
- C.
o número de observações é insuficiente para a estimação dos coeficientes.
- D.
pode haver problemas de heterocedasticidade na estimação.
- E.
há autorrelação dos resíduos.
Observações de duas variáveis econômicas, Y e X, satisfazem o modelo linear: , onde ei é o erro aleatório com as suposições usuais. O método de mínimos quadrados aplicado a uma amostra de tamanho 100 produziu o modelo ajustado:
400 + 0,8X
Sendo o desvio padrão do coeficiente β estimado em 1 e a soma dos quadrados dos resíduos é igual a 588, o estimador não-viesado da variância do erro é
- A. 0,1
- B. 1
- C. 3,5
- D. 4
- E. 6
Considere um modelo de regressão simples conforme especificado abaixo: Yi = a + bXi + ui e (i = 1,2...n), onde Yi é a variável dependente, Xi a variável explicativa, ui é o termo aleatório, a e b são os parâmetros e n indica o tamanho da amostra. Marque a alternativa que NÃO corresponde a um pressuposto do modelo de regressão linear simples:
- A.
Aleatoriedade do termo aleatório.
- B.
Média diferente de zero do termo aleatório.
- C.
Homocedasticidade.
- D.
O termo aleatório tem distribuição normal.
- E.
Independência entre o termo aleatório e a variável explicativa.


