Questões sobre Teste de Hipótese

Em uma cidade é realizada uma pesquisa sobre a preferência dos eleitores com relação a um determinado candidato, que afirma ter 60% da preferência. Uma amostra aleatória de tamanho 600 foi extraída da população, considerada de tamanho infinito, sendo que 330 eleitores manifestaram sua preferência pelo candidato. Com base nesta amostra, deseja-se testar a hipótese H₀ : p = 60% (hipótese nula) contra H₁ : p ≠ 60% (hipótese alternativa), em que p é a proporção dos eleitores que têm preferência pelo candidato. Para a análise considerou-se normal a distribuição amostral da frequência relativa dos eleitores que têm preferência pelo candidato e que na distribuição normal padrão Z a probabilidade P(|Z| ≤ 1,96) = 95% e P(|Z| ≤ 2,58) = 99%. A conclusão é que H0

• A.

  não é rejeitada tanto ao nível de significância de 1% como ao nível de significância de 5%.

• B.

  é rejeitada ao nível de significância de 5%.

• C.

  é rejeitada ao nível de significância de 1%.

• D.

  não é rejeitada para algum nível de significância superior a 5%.

• E.

  é rejeitada para algum nível de significância inferior a 1%.

O gerente de produção de uma grande fábrica de farinha garante à sua rede de atacadistas que cada pacote produzido não contém menos de 1 kg de farinha. Um comprador desconfiado extrai uma amostra aleatória de 25 pacotes e encontra para esta amostra uma média m, em kg, e uma variância de 0,04 (kg)2. Supondo que a quantidade de farinha em cada pacote apresente uma distribuição normal com média μ e variância σ2 desconhecida, deseja-se saber se o gerente tem razão a um nível de significância de 5% com a realização do teste t de Student. Seja H0 a hipótese nula do teste (μ = 1 kg), H₁ a hipótese alternativa (μ < 1 kg) e t o valor do quantil da distribuição t de Student tal que P(|t| ≥ 1,71) = 0,05, tanto para 24 como para 25 graus de liberdade. Sabendo-se que H₀ foi rejeitada, então o valor encontrado para m foi, no máximo,

• A.

  0,8584 kg.

• B.

  0,8950 kg.

• C.

  0,9316 kg.

• D.

  0,9589 kg.

• E.

  0,9863 kg.

O dirigente de uma empresa deverá decidir entre dois candidatos, Antônio e Paulo, qual ocupará o cargo de gerente administrativo. Para cada candidato foi aplicada uma mesma prova constituída de 16 testes de assuntos diversos. Subtraindo dos escores apresentados por Antônio os respectivos escores apresentados por Paulo, observa-se a presença de sinal negativo nas diferenças dos escores de 4 testes e sinal positivo nas 12 restantes, não ocorrendo diferença nula. Aplica-se o teste dos sinais para decidir se a proporção populacional de sinais negativos (p) é igual a 0,50, ao nível de significância de 2α, considerando as hipóteses: H₀ : p = 0,50 (hipótese nula) e H₁ : p ≠ 0,50 (hipótese alternativa). Aproximando a distribuição binomial pela normal, obteve-se o escore reduzido r correspondente para comparação com o valor crítico z da distribuição normal padrão (Z) tal que P(|Z| ≤ z) = 2α. Então,

• A.

  r = −2,00.

• B.

  r = −0,80.

• C.

  r = 0,50.

• D.

  r = 0,80.

• E.

  r = 2,00.

Considere que houve interesse em comparar a eficácia de 3 métodos de treinamento para uma profissão e que os candidatos foram escolhidos por sorteio e divididos em 3 grupos, com 10 elementos cada um.

− GRUPO I: recebeu treinamento à distância, pela Internet.

− GRUPO II: recebeu treinamento no local de trabalho com instrutor.

− GRUPO III: recebeu treinamento por instrução programada.

Após o término dos 3 métodos de treinamento, foi aplicado um teste com notas variando de 0 a 10 para todos os candidatos. Pelo quadro de análise de variância, obteve-se os seguintes resultados com relação às notas apresentadas pelos candidatos:

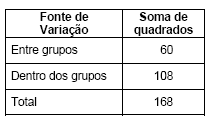
Para testar a hipótese da existência de reais diferenças na eficácia dos métodos foi calculado o valor da estatística F para comparação com o F tabelado (variável F de Snedecor com m graus de liberdade no numerador e n graus de liberdade no denominador). O valor calculado da estatística F foi de

• A.

  4,0.

• B.

  4,5.

• C.

  5,0.

• D.

  6,0.

• E.

  7,5.

A proporção de pessoas favoráveis a um certo projeto governamental é p. Sorteiam-se ao acaso, e com reposição, 400 pessoas. Calcula-se a proporção pˆ de pessoas favoráveis ao projeto na amostra. Deseja-se testar:

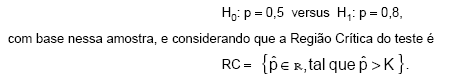
Fazendo uso do Teorema do Limite Central, o valor de K para que a probabilidade do erro tipo I seja igual à probabilidade do erro tipo II é

• A.

  4/5

• B.

  3/5

• C.

  5/6

• D.

  2/3

• E.

  5/8

Considere a função densidade de probabilidade da variável X dada por:

Para testar as hipóteses

H0: φ = 1 versus H1: φ = 2, com base numa única observação, decidiu-se rejeitar H0 se X ≤ 0,8. Supondo que o valor observado para x foi 0,4, o nível descritivo e o poder do teste são dados respectivamente por

• A.

  (0,4)⁴ e 0,64

• B.

  (0,4)² e 0,8

• C.

  (0,4)³ e 0,64

• D.

  (0,4)⁴ e 0,8

• E.

  0,4 e 0,8

Da Teoria de Testes de Hipóteses sabe-se que:

I. O nível de significância () é a chance de errar ao decidir pela hipótese H₀.

II. Quanto maior o nível de significância menos confiáveis serão os resultados da inferência estatística.

Considerando as assertivas acima, pode-se afirmar que:

• A.

  Somente a I é verdadeira.

• B.

  Ambas são falsas.

• C.

  Somente a II é verdadeira.

• D.

  Ambas são verdadeiras.

Em relação a Testes de Hipóteses sabe-se que:

I. A inferência estatística tem 100% de certeza de estar correta.

II. Existem dois tipos de erros: Erro tipo I e o Erro tipo II.

III. A probabilidade do Erro tipo II é igual a ß, considera-se que (1- ß) é o poder do teste.

Considerando as assertivas acima, pode-se afirmar que:

• A.

  Apenas I e II são verdadeiras.

• B.

  Todas são verdadeiras.

• C.

  Apenas I e III são verdadeiras.

• D.

  Apenas II e III são verdadeiras.

Uma instituição está avaliando uma nova proposta de controle de fluxo interno de documentos. Um fluxo é considerado adequado quando um documento é expedido em no máximo 1 dia, e no atual controle de fluxo sabe-se que isso ocorre em 50% dos documentos. A nova proposta foi observada em 25 documentos e observou-se que 60 % foram expedidos no tempo considerado adequado. Considerando um nível de significância de 5%, estatisticamente pode-se recomendar que:

• A.

  Permaneça com o controle atual.

• B.

  Troque para a nova proposta.

• C.

  Tanto faz, um ou outro controle.

• D.

  Nada se pode afirmar.

Uma instituição está avaliando o tempo de recuperação de processos arquivados. O Setor de Arquivamento apresentou uma nova proposta que julga melhor que a atual forma de recuperação, pois esta leva em média 5 dias. A nova proposta foi observada na recuperação de 100 documentos e observou-se um tempo médio de 4 dias e desvio-padrão de 2 dias. Considerando um nível de significância de 5%, estatisticamente pode-se recomendar que:

• A.

  nada se pode afirmar.

• B.

  tanto faz, uma ou outra forma.

• C.

  permaneça com a recuperação atual.

• D.

  troque para a nova proposta.