Questões sobre Teste de Hipótese

Para que um município possa participar de um projeto na área educacional, a média das notas dos estudantes de 5.ª série a 8.ª série das escolas públicas localizadas nesse município deverá ser igual ou superior a 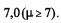  Como não foi possível coletar os dados de todos os estudantes, retirou-se uma amostra aleatória simples de 625 estudantes. Por um teste estatístico, não há evidências estatísticas contra a hipótese de que as notas dos estudantes seguem uma distribuição normal. A nota média observada na amostra foi igual a 6,5 e o desvio padrão amostral foi igual a 2,5. Considerando a situação hipotética apresentada no texto, julgue os itens que se seguem.

O teste de aderência baseada na estatística qui-quadrado é apropriado para avaliar a hipótese de que as notas dos estudantes seguem uma distribuição normal.

• C. Certo
• E. Errado

Com relação ao texto e considerando que a amostra de 100 dias seja aleatória simples, julgue os próximos itens.

Considere as hipóteses nula e alternativa, dadas respectivamente por H₀: m = 25 e H_A: m 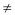25, em que m representa a média populacional. Pelo teste t, há fortes evidências para se rejeitar H₀.

• C. Certo
• E. Errado

O custo mensal de manutenção C de um aparelho é uma variável aleatória normalmente distribuída com variância populacional igual a 900 (R$)². Para testar a hipótese nula H₀ : μ = R$ 175,00 contra a alternativa H1 : μ ≠ R$175,00 será usada uma amostra de 36 aparelhos (μ é a média da população). Fixando-se o nível de significância (α) em 5%, considerando a população de tamanho infinito e sabendo que na distribuição normal padrão (Z) a probabilidade P(Z > 2) = 2,5%, rejeita-se H₀ caso a média da amostra seja

• A.

  inferior a R$ 167,00.

• B.

  superior a R$ 167,00 e inferior a R$ 187,00.

• C.

  igual a R$ 184,00.

• D.

  superior a R$ 115,00 e inferior a R$ 235,00.

• E.

  inferior a R$ 165,00 ou superior a R$ 185,00.

Um grande fabricante de farinha em uma cidade alega que cada pacote produzido pela sua fábrica não contém menos que 1 kg de farinha. Uma amostra de 16 pacotes apresentou uma média de 0,9 kg e desvio padrão de 0,1 kg. Supondo que a quantidade de farinha em cada pacote tenha uma distribuição normal com média μ e variância desconhecida, deseja-se saber se o fabricante tem razão a um determinado nível de significância α. Seja H₀ a hipótese nula do teste (μ = 1 kg), H₁ a hipótese alternativa (μ < 1 kg) e t_α < 0 o quantil da distribuição t de Student, no nível de significância α, para teste unicaudal com 15 graus de liberdade. Sabendo-se que pelo teste t de Student H₀ foi rejeitada, então

• A.

  tem-se que H₀ seria rejeitada para qualquer nível de significância, pois 0,9 < 1.

• B.

  para um nível de significância β, tal que β > α, H₀ não seria rejeitada.

• C.

  o valor da estatística obtido por meio da amostra para comparação com t_α é igual a − 1.

• D.

  o número de graus de liberdade, no caso, não interfere na obtenção de t_α.

• E.

  

Um fabricante divulga que a característica principal de seu produto tem uma média de 1 000 unidades. Um pesquisador, duvidando desta afirmação, encontrou uma característica média de 935 e desvio-padrão amostral de 130 examinando uma amostra aleatória simples de tamanho 9 destes produtos. Calcule o valor mais próximo da estatística t para testar a hipótese nula de que a média da característica principal do produto é 1 000, admitindo que a característica tem uma distribuição normal.

• A.

  -1,5.

• B.

  -1,78.

• C.

  -1,89.

• D.

  -1,96.

• E.

  -2,115.

A análise de variância de um modelo estatístico de regressão linear ordinária com uma variável dependente, um termo constante mais três variáveis como regressores, forneceu uma soma dos quadrados devido à regressão de 13 590 e uma soma dos quadrados dos resíduos de 6 795. Dado que foram usadas 14 observações, calcule o valor mais próximo da estatística F para o teste de hipótese da não-existência da regressão linear estudada.

• A.

  2.

• B.

  5.

• C.

  6,67.

• D.

  7.5.

• E.

  10.

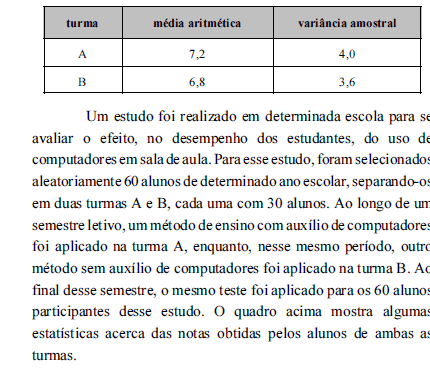
Considerando essas informações, acerca de probabilidade, inferência e amostragem, julgue os itens a seguir.

Sob a hipótese nula de que as distribuições das notas de ambas as turmas são normais e identicamente distribuídas, a estatística do teste t para a comparação dessas duas médias amostrais segue uma distribuição t de Student com 58 graus de liberdade.

• C. Certo
• E. Errado

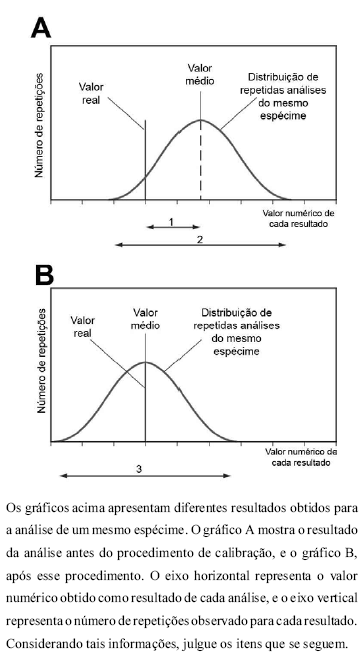
Para que se possa realizar o teste e elaborar os gráficos mostrados é necessário que se conheça previamente o resultado correto esperado para a análise realizada.

• C. Certo
• E. Errado

A melhor estimativa para o tempo médio 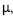sob a hipótese de que o processo está sob controle, é um valor superior a 16 min e inferior a 18 min.

• C. Certo
• E. Errado

O P-valor do teste é superior a 2%.

• C. Certo
• E. Errado