Questões sobre Teste de Hipótese

Em relação a Testes de Hipóteses sabe-se que existem os métodos paramétricos e os não-paramétricos. Sabe-se que:

I. Os teste paramétricos supõem que os dados se distribuem Normalmente.

II. Os testes não paramétricos são aplicados a dados com nível de mensuração qualitativa.

 

Considerando as assertivas acima, pode-se afirmar que:

• A.

  ambas são falsas.

• B.

  ambas são verdadeiras.

• C.

  somente a II é verdadeira.

• D.

  somente a I é verdadeira.

As questões de n^os 57 a 59 referem-se aos resultados de um teste de associação entre as variáveis representadas na tabela de contingência a seguir.

O valor da estatística qui-quadrado e o nível descritivo do teste (p-value) observados foram, respectivamente, X ²=1,811 e 0,770.

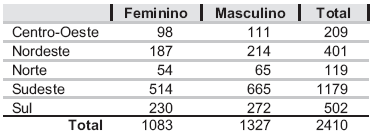
Com relação ao teste de hipótese realizado, considere as afirmações a seguir.

I - O teste foi baseado em 9 graus de liberdade.

II - A hipótese de independência entre Sexo e Região não é rejeitada para qualquer nível de significância inferior a 10,0%.

III - Com 95,0% de confiança afirma-se que existe associação entre as variáveis Sexo e Região.

IV - Sob a hipótese de independência entre as variáveis Sexo e Região, o número esperado de mulheres na região Norte é menor que o número observado.

Estão corretas APENAS as afirmações

• A.

  I e II

• B.

  II e IV

• C.

  II e IV

• D.

  I, III e IV

• E.

  II, III e IV

As questões de n^os 57 a 59 referem-se aos resultados de um teste de associação entre as variáveis representadas na tabela de contingência a seguir.

O valor da estatística qui-quadrado e o nível descritivo do teste (p-value) observados foram, respectivamente, X ²=1,811 e 0,770.

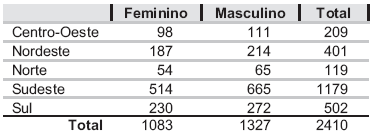
No cálculo da estatística do teste, a menor diferença entre o número de homens observado e o esperado ocorre na região

• A.

  Centro-Oeste

• B.

  Nordeste

• C.

  Sudeste

• D.

  Norte

• E.

  Sul

Com relação aos testes de hipótese sobre um parâmetro de uma população, baseados em uma amostra de tamanho n dessa população, afirma-se que

I - o poder do teste aumenta com 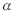 a probabilidade de um erro do tipo I, n mantido constante;

II - o poder do teste não depende de n;

III - o poder do teste é a probabilidade de o teste rejeitar uma hipótese H₀ quando esta é falsa;

IV- o poder do teste é igual a 1 − 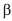 , onde  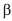é a probabilidade de um erro do tipo II;

Estão corretas APENAS as afirmações

• A.

  I e IV

• B.

  II e III

• C.

  I, II e III

• D.

  I, III e IV

• E.

  II, III e IV

Considere as asserções a seguir.

A região de rejeição de um teste de hipóteses é obtida sob a suposição de que a hipótese da nulidade (H₀) é verdadeira.

PORQUE

Em testes de hipóteses, o erro do tipo I é aquele cometido ao se rejeitar a hipótese da nulidade (H₀) quando esta é verdadeira.

Analisando-se as asserções, conclui-se que

• A.

  as duas asserções são verdadeiras, e a segunda é uma justificativa correta da primeira.

• B.

  as duas asserções são verdadeiras, e a segunda não é uma justificativa correta da primeira.

• C.

  a primeira asserção é verdadeira, e a segunda é falsa.

• D.

  a primeira asserção é falsa, e a segunda é verdadeira.

• E.

  a primeira e a segunda asserções são falsas.

Texto para as questões de 36 a 38

Um pequeno levantamento estatístico foi realizado em dois locais diferentes de atendimento ao público com o objetivo de estimar o número médio de pessoas que diariamente são atendidas nesses locais. Em dez dias de observação, foi registrado o seguinte:

Considere-se a seguinte hipótese nula: os números acima são realizações independentes de uma distribuição de Poisson com média igual a μ, e as observações são pareadas (isto é, em um mesmo dia d foram registrados os números de pessoas atendidas no local X e no local Y).

Ainda com base nas informações apresentadas no texto, assinale a opção correta acerca de testes de hipóteses para comparações entre duas médias.

• A. Embora a distribuição do número de pessoas não seja hipoteticamente normal, o teste t para dados pareados pode ser utilizado para se testar a hipótese apresentada no texto.
• B.

  Considere-se a hipótese alternativa como: "o número médio de pessoas que diariamente são atendidas no local Y é maior do que no local X". Se o teste t para a comparação de médias entre duas populações independentes (observações nãopareadas) for empregado, então a conclusão do teste será a de que a hipótese nula é falsa.

• C.

  Na situação apresentada no texto, o teste da razão de verossimilhança não é apropriado porque, hipoteticamente, a distribuição do número de pessoas não é normal.

• D.

  Sob a hipótese nula, a estimativa do erro padrão da média é inferior a 0,3.

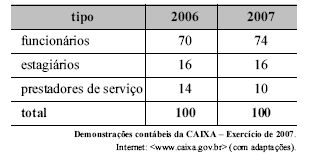
Considerando a tabela acima, que apresenta a distribuição do quadro de colaboradores da CAIXA, em mil pessoas, no final dos anos de 2006 e 2007, julgue os itens seguintes.

Considerando que, para se testar a hipótese nula de que a distribuição do quadro de colaboradores de 2007 manteve-se estatisticamente igual à distribuição de 2006, seja aplicado um teste qui-quadrado, nessa situação, a estatística do teste será igual a 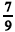 e possuirá 2 graus de liberdade.

• C. Certo
• E. Errado

A probabilidade de significância do teste é inferior a 0,02 e, portanto, hipótese nula é rejeitada caso seja fixado um nível de significância superior a 2%.

• C. Certo
• E. Errado

O poder do teste, que representa a probabilidade de se aceitar corretamente a hipótese nula, é igual a 98,2%.

• C. Certo
• E. Errado

Uma instituição lançará uma campanha nacional entre as indústrias brasileiras com o objetivo de reduzir a probabilidade de ocorrência de acidentes de trabalho. Atualmente, a probabilidade de um operário sofrer algum tipo de acidente é igual a 0,06. Após o lançamento da campanha, espera-se que a probabilidade de um operário sofrer algum tipo de acidente passe a ser inferior a 0,02. Antes de essa empresa lançar a campanha em âmbito nacional, ela realizou um estudo-piloto em um pequeno número de indústrias, adotando o seguinte plano amostral. De um cadastro de indústrias, foram selecionadas aleatoriamente 2 indústrias e nelas aplicaram-se as campanhas propostas pela instituição, envolvendo todos os operários que lá trabalhavam na ocasião do estudo. Essas indústrias são chamadas "caso". Também foram selecionadas aleatoriamente outras 2 indústrias, mas nelas as campanhas não foram aplicadas. Essas são chamadas "controle". Ao longo de um ano foram registrados os números de operários que sofreram algum tipo de acidente nas quatro indústrias, segundo a tabela abaixo.

Com base nas informações apresentadas no texto e na tabela, julgue os itens que se seguem.

Considere-se que a ocorrência de acidentes segue uma distribuição de Poisson e a hipótese nula (H0) do teste é: "a probabilidade de um operário sofrer algum tipo de acidente é igual a 0,06, mas se um operário for exposto à campanha, a probabilidade de ele, operário, sofrer algum tipo de acidente é reduzida para 0,02". A hipótese alternativa (Ha) é: "a probabilidade de um operário sofrer algum tipo de acidente é igual a 0,06, independentemente de o operário ter sido ou não exposto à campanha". Nessa situação, se a estatística qui-quadrado sob H0 for igual a Q0 e se a estatística qui-quadrado sob Ha for igual a Qa, então é correto afirmar que a razão Q0/Qa é a estatística de razão de verossimilhança para o teste em questão.

• C. Certo
• E. Errado