Questões de Estatística da Fundação CESGRANRIO (CESGRANRIO)

A teoria da probabilidade permite que se calcule a chance de ocorrência de um número em um experimento aleatório. Considerando a teoria das probabilidades analise as afirmações abaixo.

I - Experimentos mutuamente excludentes são aqueles cujos elementos integrantes apresentam características únicas e os resultados possíveis não serão previsíveis.

II - Experimento aleatório é aquele cujo resultado é imprevisível, porém pertence necessariamente a um conjunto de resultados possíveis denominado espaço amostral.

III - Qualquer subconjunto do espaço amostral é denominado evento, sendo que, se esse subconjunto possuir apenas um elemento, o denominamos evento elementar.

É(São) correta(s) a(s) afirmativa(s)

• A.

  I, apenas.

• B.

  II, apenas.

• C.

  I e II, apenas.

• D.

  II e III, apenas.

• E.

  I, II e III.

Relacione os conceitos probabilísticos às suas definições.

Estão corretas as associações

• A. I – S ; II – Q e III – P.
• B.

  I – S ; II – P e III – Q.

• C.

  I – P ; II – Q e III – S.

• D.

  I – R ; II – P e III – Q.

• E.

  I – Q ; II – P e III – R.

Experimentos aleatórios são considerados como fenômenos produzidos pelo homem, como, por exemplo, a determinação da vida útil de um componente eletrônico, o lançamento de um dado, o lançamento de uma moeda honesta e a retirada de uma carta de um baralho completo de 52 cartas.

Sobre experimentos aleatórios, considere as proposições a seguir.

I – Cada experimento poderá ser repetido indefinidamente sob as mesmas condições.

II – Não se conhece um particular valor do experimento a priori, porém pode-se descrever todos os possíveis resultados.

III – Para a explicação desses fenômenos aleatórios adota-se um modelo matemático probabilístico.

IV – Quando o experimento for repetido um grande número de vezes surgirá uma regularidade.

São corretas as proposições

• A.

  I e II, apenas.

• B.

  III e IV, apenas.

• C.

  I, II e III, apenas.

• D.

  II, III e IV, apenas.

• E.

  I, II, III e IV.

Sejam os gráficos (Box-plots) a seguir.

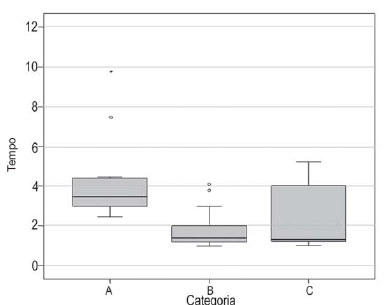
Considerando que 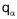 corresponde ao  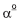quartil da distribuição, conclui-se que

• A.

  a mediana da classe B é superior ao terceiro quartil da distribuição C.

• B.

  a distribuição A apresenta o maior desvio interquartílico, quando comparado às demais distribuições.

• C.

  

• D.

  

• E.

  todas as distribuições apresentam assimetria negativa.

Leia o texto abaixo para responder às questões de nos 21 e 22.

O histograma a seguir representa dados de uma determinada amostra, sendo que, no eixo horizontal, estão representados os pontos médios das classes, todas com a mesma amplitude e, no eixo vertical, as frequências relativas.

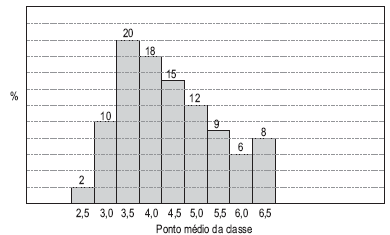
A probabilidade de um valor escolhido estar entre 4,25 e 6,25 é

• A.

  68%

• B.

  60%

• C.

  55%

• D.

  48%

• E.

  42%

Leia o texto abaixo para responder às questões de nos 21 e 22.

O histograma a seguir representa dados de uma determinada amostra, sendo que, no eixo horizontal, estão representados os pontos médios das classes, todas com a mesma amplitude e, no eixo vertical, as frequências relativas.

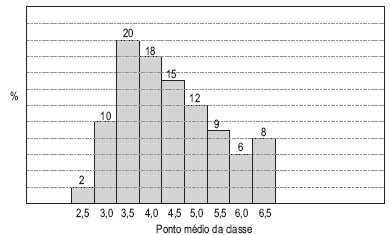
A estimativa obtida, por interpolação linear, para o valor que acumula uma probabilidade de no máximo 10% é

• A.

  3,25

• B.

  3,15

• C.

  3,00

• D.

  2,80

• E.

  2,75

Lança-se uma moeda honesta três vezes. Sejam os eventos:

A = {sair duas caras ou três caras} e

B = {os dois primeiros resultados são iguais}

Nessas condições, tem-se que

• A.

  P(A) = 0,25; P(B) = 0,25; A e B não são independentes e não são mutuamente exclusivos.

• B.

  P(A) = 0,25; P(B) = 0,25; A e B são independentes e não são mutuamente exclusivos.

• C.

  P(A) = 0,5; P(B) = 0,25; A e B não são independentes e não são mutuamente exclusivos.

• D.

  P(A) = 0,5; P(B) = 0,5; A e B são independentes e não são mutuamente exclusivos.

• E.

  P(A) = 0,5; P(B) = 0,5; A e B não são independentes e não são mutuamente exclusivos.

Dado um indivíduo com 50 anos, a probabilidade de morrer antes de completar 55 anos é de, aproximadamente,

• A.

  3,8%

• B.

  4,7%

• C.

  8,8%

• D.

  95,3%

• E.

  96,2%

Segundo a Pesquisa Nacional por Amostra de Domicílios – PNAD-2008, aproximadamente 30% dos domicílios brasileiros possuíam microcomputador, sendo que 22% desses tinham acesso à Internet. Restringindo a população aos domicílios com rendimento mensal superior a 20 salários mínimos (que representavam 5% do total), as porcentagens alteraram para 90% e 80%, respectivamente. Selecionando-se aleatoriamente um domicílio dessa amostra, a renda mensal domiciliar observada foi inferior a 20 salários mínimos; então, a probabilidade de ele possuir microcomputador e ter acesso à Internet é

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Seja X uma variável aleatória não negativa do tipo contínuo, tal que F_X(p_0,90) = 0,90. Considere uma amostra aleatória de tamanho n de X. Se X₍₁₎ e X_(n) são as estatísticas de ordem mínimo e máximo da amostra, respectivamente, então 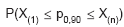é

• A.

  1 − (0,90)ⁿ

• B.

  1 − (0,90)ⁿ − (0,10)ⁿ

• C.

  (0,90)ⁿ

• D.

  (0,90)ⁿ − (0,10)ⁿ

• E.

  (0,90)ⁿ + (0,10)ⁿ