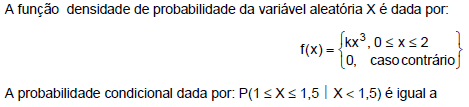Questões de Estatística da Fundação Carlos Chagas (FCC)

• A.

  7/9.

• B.

  7/12.

• C.

  2/3.

• D.

  5/12.

• E.

  5/9.

Os estimadores não viesados E₁, E₂ e E₃, dados abaixo, são utilizados para obtenção da média μ diferente de zero de uma população normal com variância unitária. Considere que (X, Y, Z) é uma amostra aleatória, com reposição, de tamanho 3 desta população, com m, n e p sendo parâmetros reais.

E₁ = mX + nY + pZ

E₂ = 2mX + 2nY + pZ

E₃ = mX + 2nY + 2pZ

A soma das variâncias de E₁, E₂ e E₃ é igual a

• A.

  12.

• B.

  15.

• C.

  18.

• D.

  21.

• E.

  24.

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Em uma empresa trabalham 125 funcionários, sendo 45 com nível superior e 80 com nível médio. A média aritmética dos salários dos funcionários com nível superior supera a dos funcionários com nível médio em R$ 1.750,00 e a média aritmética de todos os 125 funcionários é igual a R$ 2.880,00. O valor da soma da média aritmética dos salários dos funcionários com nível superior com a média aritmética dos salários dos funcionários com nível médio é

• A.

  R$ 6.000,00.

• B.

  R$ 6.250,00.

• C.

  R$ 6.500,00.

• D.

  R$ 6.750,00.

• E.

  R$ 7.000,00.

Sejam os estimadores E₁ = (m−4)X − (2m−4) + (m+1)Z e E₂ = 2m + (2−m)Y − (m+1)Z da média μ diferente de zero de uma população normal com variância unitária. A amostra aleatória (X, Y, Z) de tamanho 3 foi extraída, com reposição, desta população e m é um parâmetro real. O menor valor inteiro de m, tal que E₁ é mais eficiente que E₂, é

• A.

  0.

• B.

  1.

• C.

  2.

• D.

  3.

• E.

  4.

Sabe-se que 80% de todos os eleitores de uma grande cidade brasileira são favoráveis que se aplique, nas próximas eleições, a Lei da Ficha Limpa. Se 4 eleitores são selecionados ao acaso e com reposição dentre todos os eleitores dessa cidade, a probabilidade de que pelo menos 3 sejam favoráveis que a referida lei seja aplicada nas próximas eleições é

• A.

  0,8192.

• B.

  0,8150.

• C.

  0,8012.

• D.

  0,7896.

• E.

  0,7894.

• A.

  12.

• B.

  15.

• C.

  18.

• D.

  21.

• E.

  24.

Numa determinada zona eleitoral sabe-se que 40% dos eleitores são do sexo masculino. Entre estes, 10% têm curso superior ao passo que entre os eleitores do sexo feminino, 25% têm curso superior. Selecionando-se um eleitor ao acaso, a probabilidade de que ele seja do sexo feminino ou não tenha curso superior é

• A.

  0,68.

• B.

  0,79.

• C.

  0,81.

• D.

  0,96.

• E.

  0,98.

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Suponha que o número de eleitores que chegam a uma seção de uma Zona Eleitoral no dia de uma determinada eleição, siga a uma distribuição de Poisson com uma média de chegada de 30 eleitores por meia hora. A probabilidade de que cheguem menos de 3 eleitores em 5 minutos é

• A.

  12,5 e⁻⁵.

• B.

  12,5 e⁻⁶.

• C.

  18,5 e⁻⁵.

• D.

  17,5 e⁻⁵.

• E.

  17,5 e⁻⁶.