Questões de Matemática

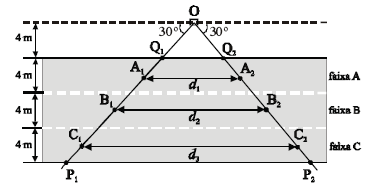
O esquema acima ilustra um radar rodoviário, posicionado no ponto O, a 4 m de distância de uma das bordas de uma rodovia de três faixas retilíneas e paralelas, de 4 m de largura cada. Nesse esquema, a região triangular de vértices O, P₁ e P₂ é a área de cobertura do radar. O radar detecta o instante em que o automóvel entra na área de cobertura, em um dos pontos A₁, B₁ ou C₁, e o instante em que ele deixa essa área, em um dos pontos A₂, B₂ ou C₂, e registra o tempo gasto em cada um desses percursos. Como as distâncias d₁, d₂ e d₃ são preestabelecidas, o radar calcula a velocidade média desenvolvida pelo veículo nesse percurso, dividindo a distância percorrida pelo tempo gasto para percorrê-la, dependendo da faixa em que o veículo se encontra. Os pontos A₁, B₁ e C₁ distam 2 m das bordas de cada uma das faixas A, B e C, respectivamente, e os segmentos de reta A₁A₂, B₁B₂ e C₁C₂ são paralelos às bordas da rodovia.

Com base no esquema apresentado e nas condições estabelecidas, julgue os itens a seguir.

Se um automóvel, deslocando-se pela faixa B, leva 2 s para percorrer o trajeto correspondente ao segmento B₁B₂, então a sua velocidade média nesse percurso é inferior a 60 km/h.

• C. Certo
• E. Errado

Três sarrafos medem, respectivamente, 12 m, 18 m e 30 m. Um carpinteiro quer dividi-los em partes menores de forma que todas tenham o mesmo comprimento e sejam do maior tamanho possível. Além disso, ele não quer que sobre nenhum pedaço de madeira. Nessa situação, o carpinteiro

obterá mais de 10 pedaços de madeira após as divisões corretas dos sarrafos.

• C. Certo
• E. Errado

As autoridades de uma cidade, visando estabelecer regras para as construções residenciais, estabeleceram as seguintes normas:

I o espaço ocupado pelas edificações — casa, piscina, canil, garagem etc. — não deve ultrapassar a 80% da área total do terreno;

II as edificações não poderão invadir a faixa de 1 m de largura até os limites do terreno.

Com base nessas regras, considere um terreno retangular, medindo 15 m de frente e 45 m na lateral, onde serão executadas obras de uma edificação, e julgue os itens que se seguem.

A soma das áreas que podemser ocupadas por todas as edificações nesse terreno é inferior a 520 m2.

• C. Certo
• E. Errado

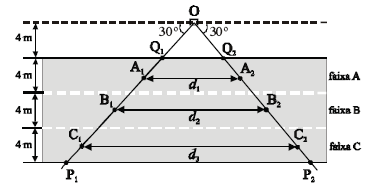
O esquema acima ilustra um radar rodoviário, posicionado no ponto O, a 4 m de distância de uma das bordas de uma rodovia de três faixas retilíneas e paralelas, de 4 m de largura cada. Nesse esquema, a região triangular de vértices O, P₁ e P₂ é a área de cobertura do radar. O radar detecta o instante em que o automóvel entra na área de cobertura, em um dos pontos A₁, B₁ ou C₁, e o instante em que ele deixa essa área, em um dos pontos A₂, B₂ ou C₂, e registra o tempo gasto em cada um desses percursos. Como as distâncias d₁, d₂ e d₃ são preestabelecidas, o radar calcula a velocidade média desenvolvida pelo veículo nesse percurso, dividindo a distância percorrida pelo tempo gasto para percorrê-la, dependendo da faixa em que o veículo se encontra. Os pontos A₁, B₁ e C₁ distam 2 m das bordas de cada uma das faixas A, B e C, respectivamente, e os segmentos de reta A₁A₂, B₁B₂ e C₁C₂ são paralelos às bordas da rodovia.

Com base no esquema apresentado e nas condições estabelecidas, julgue os itens a seguir.

A área da parte da rodovia que está dentro da área de cobertura do radar, que tem como vértices os pontos P₁, P₂, Q₂ e Q₁, é igual a .

• C. Certo
• E. Errado

Três sarrafos medem, respectivamente, 12 m, 18 m e 30 m. Um carpinteiro quer dividi-los em partes menores de forma que todas tenham o mesmo comprimento e sejam do maior tamanho possível. Além disso, ele não quer que sobre nenhum pedaço de madeira. Nessa situação, o carpinteiro

deve dividir os sarrafos em partes que tenham 6 m de comprimento cada.

• C. Certo
• E. Errado

O tanque do automóvel de Cláudio tem a forma de um paralelepípedo retângulo que mede, internamente, 20 cm de altura, 40 cm de largura e 80 cm de comprimento. O automóvel de Cláudio consome 1 L de gasolina a cada 12 km rodados, com o ar condicionado desligado. Ligando o ar condicionado, o consumo passa a ser de 1 L para cada 10 km rodados.

A respeito da situação hipotética acima e do automóvel de Cláudio, julgue os seguintes itens.

O tanque do automóvel de Cláudio tem capacidade para mais de 70 L de gasolina.

• C. Certo
• E. Errado

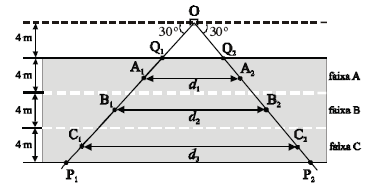
O esquema acima ilustra um radar rodoviário, posicionado no ponto O, a 4 m de distância de uma das bordas de uma rodovia de três faixas retilíneas e paralelas, de 4 m de largura cada. Nesse esquema, a região triangular de vértices O, P₁ e P₂ é a área de cobertura do radar. O radar detecta o instante em que o automóvel entra na área de cobertura, em um dos pontos A₁, B₁ ou C₁, e o instante em que ele deixa essa área, em um dos pontos A₂, B₂ ou C₂, e registra o tempo gasto em cada um desses percursos. Como as distâncias d₁, d₂ e d₃ são preestabelecidas, o radar calcula a velocidade média desenvolvida pelo veículo nesse percurso, dividindo a distância percorrida pelo tempo gasto para percorrê-la, dependendo da faixa em que o veículo se encontra. Os pontos A₁, B₁ e C₁ distam 2 m das bordas de cada uma das faixas A, B e C, respectivamente, e os segmentos de reta A₁A₂, B₁B₂ e C₁C₂ são paralelos às bordas da rodovia.

Com base no esquema apresentado e nas condições estabelecidas, julgue os itens a seguir.

Os valores d₁ e d₃ satisfazem à equação 7d₁ – 3d₃ = 0.

• C. Certo
• E. Errado

Em certa cidade, o preço de uma corrida de táxi é formado por duas parcelas: uma fixa, chamada de bandeirada, e outra proporcional à distância percorrida. O preço da bandeirada aumentou de 20% e o preço do quilômetro rodado aumentou de 10%, o que fez com que uma corrida que custava R$ 10,00 passasse a custar R$ 11,50. Quanto passará a custar uma corrida que custava R$ 26,00?

• A.

  R$ 28,60

• B.

  R$ 29,10

• C.

  R$ 29,60

• D.

  R$ 29,90

• E.

  R$ 31,20

Um determinado cometa A visita a Terra a cada 46 anos. Sua passagem por aqui foi em 1996. Quantas vezes ele visitou a Terra desde o nascimento de Cristo e em que ano foi sua primeira passagem na era cristã? (Era cristã depois do ano 0.)

• A. 43 vezes e o primeiro ano foi no ano 36.
• B. 44 vezes e o primeiro ano foi no ano 15.
• C. 44 vezes e o primeiro ano foi no ano 16.
• D. 44 vezes e o primeiro ano foi no ano 17.
• E. 44 vezes e o primeiro ano foi no ano 18.

"A água é um recurso finito e não tão abundante quanto pode parecer, por isso deve ser economizada." NOVA ESCOLA, Editora Abril, Junho/Julho de 2004, p.50

"Não desperdice água potável. Um furo do tamanho da cabeça de um alfinete permite o escoamento de 3200 litros de água por dia." CURSO DE FORMAÇÃO DE CONDUTORES, FIEB/SENAI, Edição ano 2000

Com base nos trechos acima e considerando que um tanque com capacidade de 640m3 possua dois furos como o descrito no trecho é correto concluir que

• A.

  em três dias o tanque desperdiça 9600 litros de água.

• B.

  o tanque cheio é esvaziado em 200 dias devido a esses dois furos.

• C.

  se um dos furos for fechado o tanque passará a desperdiçar dois terços do que desperdiçava antes.

• D.

  com a quantidade de água que este tanque desperdiça com um furo, em um dia, encheríamos 16.000 copos de 200 ml.

• E.

  fechando-se um dos furos, a quantidade de água desperdiçada, em um dia, daria para encher uma piscina de 3200 m3.