Questões de Matematica

Matemática - Aritmética e Problemas - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2021

Texto 1A3-I

Aldo, produtor de uvas, dispõe de 10 trabalhadores para realizar a colheita do seu plantio. Na época adequada, para acelerar o processo de colheita, Aldo contratou mais 5 trabalhadores, que se juntaram aos 10 já existentes.

Tendo como base o texto 1A3-I, suponha que com os 10 trabalhadores originais a colheita seria realizada em 6 dias e que os 5 novos trabalhadores trabalham com a mesma eficiência dos 10 originais. Nessa situação, com as novas contratações, a colheita será realizada em

A)

B)

C)

D)

E)

# Questão 655283

Matemática - Geometria Plana - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2021

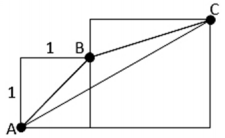
Na figura anterior, sabendo-se que a área do triângulo ABC independe do tamanho do lado do quadrado que contém o ponto C, conclui-se que a área desse triângulo é igual a

A)

B)

C)

D)

E)

# Questão 655281

Matemática - Probabilidade - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2021

Considere que, quando Carlos, agente de pesquisas por telefone, realiza uma chamada telefônica, a chance de que a sua chamada não seja atendida seja de 20% e que, se a chamada for atendida, a chance de que ele obtenha respostas verdadeiras seja de 60%. Nessa situação, a probabilidade de Carlos obter respostas verdadeiras em uma dada chamada telefônica é igual a

A)

B)

C)

D)

E)

# Questão 653528

Matemática - Aritmética e Problemas - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2021

Foi modelado que o espalhamento de uma notícia em uma população entendido como o percentual de indivíduos dessa população que recebe essa notícia por unidade de tempo é diretamente proporcional ao percentual de indivíduos da população que já conhecem a notícia multiplicado pelo percentual de indivíduos dessa população que ainda não a conhecem até aquele instante. A constante k de proporcionalidade depende, entre outros fatores, do impacto da notícia na vida dos envolvidos e de propriedades dos meios de comunicação disponíveis.

Tendo como base essas informações e considerando que, para certa notícia, k = 1, julgue o item seguinte.

Se, em determinado instante, 30% da população já conhece a notícia, então, nesse instante, o seu espalhamento estaria em patamar superior a 20% por unidade de tempo.

# Questão 653527

Matemática - Aritmética e Problemas - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2021

Foi modelado que o espalhamento de uma notícia em uma população entendido como o percentual de indivíduos dessa população que recebe essa notícia por unidade de tempo é diretamente proporcional ao percentual de indivíduos da população que já conhecem a notícia multiplicado pelo percentual de indivíduos dessa população que ainda não a conhecem até aquele instante. A constante k de proporcionalidade depende, entre outros fatores, do impacto da notícia na vida dos envolvidos e de propriedades dos meios de comunicação disponíveis.

Tendo como base essas informações e considerando que, para certa notícia, k = 1, julgue o item seguinte.

Se, em determinado instante, o espalhamento de uma notícia é igual a 16% por unidade de tempo, então, nesse instante, mais de 75% da população ainda desconhece a notícia.

# Questão 653526

Matemática - Aritmética e Problemas - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2021

Foi modelado que o espalhamento de uma notícia em uma população entendido como o percentual de indivíduos dessa população que recebe essa notícia por unidade de tempo é diretamente proporcional ao percentual de indivíduos da população que já conhecem a notícia multiplicado pelo percentual de indivíduos dessa população que ainda não a conhecem até aquele instante. A constante k de proporcionalidade depende, entre outros fatores, do impacto da notícia na vida dos envolvidos e de propriedades dos meios de comunicação disponíveis.

Tendo como base essas informações e considerando que, para certa notícia, k = 1, julgue o item seguinte.

De acordo com a modelagem realizada, é possível que, em determinado instante, o espalhamento da notícia seja superior a 50% por unidade de tempo.

# Questão 653525

Matemática - Aritmética e Problemas - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2021

Foi modelado que o espalhamento de uma notícia em uma população entendido como o percentual de indivíduos dessa população que recebe essa notícia por unidade de tempo é diretamente proporcional ao percentual de indivíduos da população que já conhecem a notícia multiplicado pelo percentual de indivíduos dessa população que ainda não a conhecem até aquele instante. A constante k de proporcionalidade depende, entre outros fatores, do impacto da notícia na vida dos envolvidos e de propriedades dos meios de comunicação disponíveis.

Tendo como base essas informações e considerando que, para certa notícia, k = 1, julgue o item seguinte.

O espalhamento de uma notícia será tanto maior quanto maior for o número de pessoas que dela tiverem tomado conhecimento.

# Questão 653524

Matemática - Álgebra - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2021

Em uma operação da PRF, foram fiscalizados: 20 veículos automotores até o fim da primeira hora; 60 veículos automotores até o fim da segunda hora; 120 veículos automotores até o fim da terceira hora; 200 veículos automotores até o fim da quarta hora; e 300 veículos automotores até o fim da quinta hora. O padrão numérico observado manteve-se até o fim da décima hora, quando, então, foi finalizada a operação.

Considerando essa situação hipotética, julgue o item seguinte.

Mais de 550 veículos terão sido fiscalizados até o fim da sétima hora de realização da operação.

# Questão 653523

Matemática - Progressões - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2021

Em uma operação da PRF, foram fiscalizados: 20 veículos automotores até o fim da primeira hora; 60 veículos automotores até o fim da segunda hora; 120 veículos automotores até o fim da terceira hora; 200 veículos automotores até o fim da quarta hora; e 300 veículos automotores até o fim da quinta hora. O padrão numérico observado manteve-se até o fim da décima hora, quando, então, foi finalizada a operação.

Considerando essa situação hipotética, julgue o item seguinte.

Considere que {q_n}, para n variando de 1 a 10, seja a sequência numérica formada pelas quantidades de veículos fiscalizados apenas no decorrer da n-ésima hora de realização da operação, ou seja, q₁ é a quantidade de veículos fiscalizados apenas no decorrer da primeira hora de realização da operação; q₂ é a quantidade de veículos fiscalizados apenas no decorrer da segunda hora de realização da operação; e assim por diante. Nessa situação, a sequência {q_n}, para n variando de 1 a 10, é uma progressão aritmética.

# Questão 664892

Matemática - Aritmética e Problemas - COPESE / UFPI - 2020

Em uma cesta existem x maçãs verdes e y maçãs vermelhas com x e y sendo números inteiros positivos. Após adicionar 15 maças verdes à cesta, o percentual da quantidade de maças verdes passou a ser 60% da quantidade total de maçãs. A opção que contém a relação correta entre x e y é:

A)

B)

C)

D)

E)

Questões de Matemática

Contato

Páginas