Questões de Matemática do ano 2009

As retas r e s de equações y = −2x + 42 e y = 3x + 12, respectivamente, representam as equações da demanda e oferta de um produto no mercado, em que y é a quantidade e x o preço do produto. A equação da reta que passa pelo ponto de intersecção de r e s (ponto de equilíbrio de mercado) e pelo ponto (a,b) no primeiro quadrante, tal que a + b = 20 e ab é o maior valor possível, é

• A.

  y = 7x + 40

• B.

  y = −7x + 20

• C.

  y = 6x + 40

• D.

  y = −5x + 60

• E.

  y = −4x + 40

Uma caixa retangular tem 46 cm de comprimento, 9 cm de largura e 20 cm de altura. Considere a maior bola que caiba inteiramente nessa caixa. A máxima quantidade de bolas iguais a essa que podem ser colocadas nessa caixa, de forma que ela possa ser tampada, é

• A.

  6

• B.

  8

• C.

  9

• D.

  10

• E.

  12

Um retângulo é tal que a soma da medida do comprimento e da medida da largura é 37 cm e cuja área é igual a 330 cm². Qual é a diferença, em centímetros, entre as medidas do comprimento e da largura deste retângulo?

• A.

  5 cm

• B.

  7 cm

• C.

  15 cm

• D.

  22 cm

• E.

  33 cm

Um aluno desenhou dois quadrados; um de lado medindo L centímetros e o outro quadrado de lado medindo (L + 2) centímetros. Observou-se que a área do maior quadrado era 20 cm² maior do que a área do quadrado menor. Então qual é a medida em centímetros do lado do maior quadrado desenhado?

• A.

  2 cm

• B.

  3 cm

• C.

  4 cm

• D.

  5 cm

• E.

  6 cm

Em uma superfície plana horizontal, uma esfera de 5 cm de raio está encostada em um cone circular reto em pé com raio da base de 5 cm e 5 cm de altura. De quantos cms é a distância entre o centro da base do cone e o ponto onde a esfera toca na superfície?

• A.

  5.

• B.

  7,5

• C.

  

• D.

  

• E.

  10

Sabe-se que, em um dado, a soma dos pontos de faces opostas é sempre igual a 7. Um dado é colocado sobre a superfície plana de uma mesa com a face "1" voltada para o leste, a "6" para o oeste, a "3" para o sul, a "4" para o norte, a "2" para cima e a "5" para baixo, da forma como é mostrado na figura seguinte.

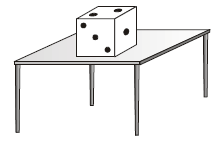
 Considere que esse dado é submetido a quatro movimentos sucessivos, cada um dos quais consiste de uma rotação de 90° em torno de uma aresta que se apóia sobre a mesa. Se após cada movimento as faces "1", "3", "5" e "6" passam a ficar, sucessivamente, voltadas para baixo, então, ao fim do quarto movimento, a face "1" estará voltada para

• A.

  baixo.

• B.

  cima.

• C.

  o norte.

• D.

  o sul.

• E.

  o oeste.

Deseja-se fabricar embalagens na forma de paralelepípedos retângulo com capacidade para 8.000 cm 3 . Nenhuma aresta da embalagem poderá medir menos que 10 cm. Uma das faces da embalagem deverá ter, pelo menos, 30 cm 2 de área. O material para a confecção das embalagens custa R$ 10,00 o metro quadrado. Com base nessas informações, julgue os itens subsequentes.

Na construção de uma embalagem cúbica que cumpre as exigências, a despesa com material será igual a R$ 2,60.

• C. Certo
• E. Errado

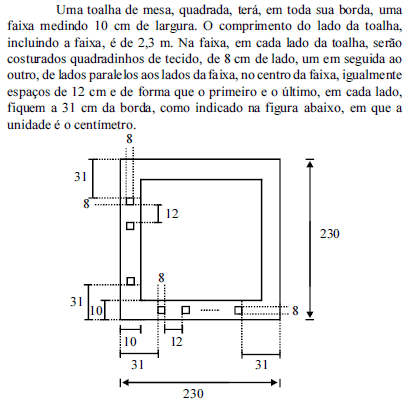
Com base nessas informações e na figura, julgue os itens que se seguem.

Se a faixa que contornará a borda da toalha for confeccionada a partir de um tecido de 10 cm de largura, então serão necessários 8,8 m desse tecido.

• C. Certo
• E. Errado

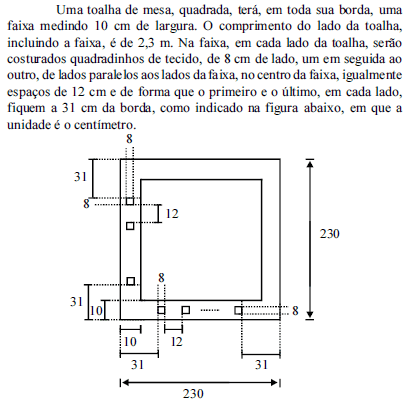
Com base nessas informações e na figura, julgue os itens que se seguem.

A área da toalha é igual a 5,29 m ²

• C. Certo
• E. Errado

            Uma toalha de mesa, quadrada, terá, em toda sua borda, uma faixa medindo 10 cm de largura. O comprimento do lado da toalha, incluindo a faixa, é de 2,3 m. Na faixa, em cada lado da toalha, serão costurados quadradinhos de tecido, de 8 cm de lado, um em seguida ao outro, de lados paralelos aos lados da faixa, no centro da faixa, igualmente espaços de 12 cm e de forma que o primeiro e o último, em cada lado, fiquem a 31 cm da borda, como indicado na figura abaixo, em que a unidade é o centímetro.

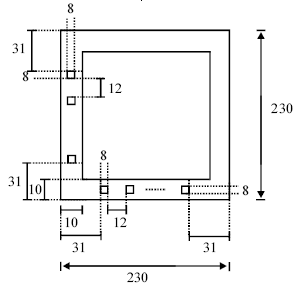
Com base nessas informações e na figura, julgue os itens que se seguem.

• C. Certo
• E. Errado