Questões de Matemática do ano 2009

Ainda em relação à questão trinta e três (33), em quantos dias ela estará totalmente curada?

• A.

  16

• B.

  8

• C.

  10

• D.

  12

• E.

  14

Com relação à questão anterior, quantas bactérias o remédio matará no 8.o dia?

• A.

  1725

• B.

  1865

• C.

  1875

• D.

  1880

• E.

  1715

Doentildes é uma menina muito doente. Ela tem hoje exatamente 230 bactérias no seu corpo que causam uma certa doença. As bactérias aumentam em número de 270 por dia. Porém, hoje, (1.o dia) ela começou a tomar um remédio que vai matar 1 bactéria. Amanhã o remédio matará 2 bactérias e assim por diante, sempre dobrando o número de bactérias mortas no dia anterior. Quantas bactérias Doentildes terá no 3.o dia?

• A.

  780

• B.

  750

• C.

  759

• D.

  763

• E.

  767

Com relação às informações apresentadas no texto acima, julgue os itens de 51 a 60.

Supondo que, em 2008, o número de telefones em serviço no Brasil fosse P₂₀₀₈ e que, a partir desse ano, ele sofresse crescimento anual à taxa de 30%, então os números P₂₀₀₈, P₂₀₀₉, ..., P_k, ..., em que P_k, k = 2008, 2009, ..., represente o número de telefones em serviço no Brasil no ano k, constituirão uma progressão geométrica de razão

• C. Certo
• E. Errado

Acerca de progressões e de funções, julgue os itens a seguir.

Considerando que a tabela a seguir indique a quantidade de atrasos de voos em seis aeroportos ao longo de quatro meses, é correto afirmar que a soma dos voos atrasados nesses 6 aeroportos nos meses de janeiro, fevereiro, março e abril formam, nessa ordem, uma progressão aritmética decrescente.

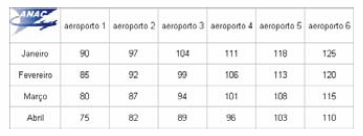
• C. Certo
• E. Errado

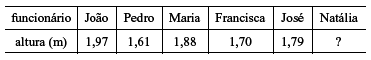
Considerando que as alturas declaradas de empregados de uma companhia aérea apresentadas na planilha acima obedeçam à lógica de uma sequência numérica, e que as alturas de Pedro, Francisca e Natália formem também outra sequência lógica, julgue os próximos itens.

A altura de Natália é igual 1,79 m.

• C. Certo
• E. Errado

Considere a sucessão dos números naturais múltiplos de 3, dispostos na seguinte forma:

0 3 6 9 1 2 1 5 1 8 2 1 2 4 2 7 3 0 3 3 3 6 3 9 . . .

Nessa sucessão, o algarismo que deve ocupar a 126a posição é

• A.

  6

• B.

  0

• C.

  1

• D.

  5

• E.

  3

Considere a seguinte sequência de figuras, formadas por triângulos pequenos.

Em cada etapa, a partir da primeira, são construídos novos triângulos pequenos sobre cada lado livre dos triângulos da figura anterior. Mantendo-se esse mesmo padrão, o número de triângulos pequenos que formarão a figura da etapa 20 é

• A.

  571

• B.

  570

• C.

  514

• D.

  513

• E.

  512

Considerando que, nos números positivos a, b, c, e d, os números a, b e d estejam, nessa ordem, em progressão geométrica; a, c e d estejam, nessa ordem, em progressão aritmética, e considerando, ainda, que a razão 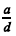seja igual a  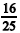e a soma dos números a, b, c e d seja 163, julgue os itens que se seguem.

O número b é maior que o número c.

• C. Certo
• E. Errado

Considerando que, nos números positivos a, b, c, e d, os números a, b e d estejam, nessa ordem, em progressão geométrica; a, c e d estejam, nessa ordem, em progressão aritmética, e considerando, ainda, que a razão 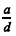seja igual a  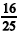e a soma dos números a, b, c e d seja 163, julgue os itens que se seguem.

A razão da progressão aritmética é menor que 8.

• C. Certo
• E. Errado