Questões de Matemática do ano 2010

Na construção de uma caixa de papelão em forma de tetraedro regular foi consumida exatamente uma folha de cartolina de 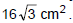 . Qual a medida da área de cada face?

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Um professor pediu que seus alunos desenhassem (com régua e compasso) em uma cartolina dura e de material com massa uniformemente distribuída um triângulo escaleno qualquer. Em seguida, o professor pediu que os alunos recortassem o triângulo e marcassem nele (usando régua e compasso) os seguintes pontos:

− ponto equidistante dos vértices do triângulo (P);

− ponto equidistante dos lados do triângulo (Q);

− centro de massa do triângulo (R).

Sabendo-se que:

− Baricentro é o encontro das três medianas;

− Circuncentro é o encontro das três mediatrizes;

− Incentro é o encontro das três bissetrizes;

− Ortocentro é o encontro das três alturas.

Alunos que resolveram corretamente o problema proposto pelo professor marcaram P, Q e R por meio das construções, respectivamente, do

• A.

  baricentro, incentro e circuncentro.

• B.

  circuncentro, incentro e ortocentro.

• C.

  ortocentro, incentro e circuncentro.

• D.

  circuncentro, incentro e baricentro.

• E.

  incentro, circuncentro e baricentro.

Um artista esculpe um cubo de pedra e, em seguida, escava em uma das faces um cone circular reto. A base circular do cone está inscrita na face do cubo, e o vértice do cone coincide com o ponto de encontro das diagonais da face oposta à face escavada do cubo. Uma planificação adequada da superfície externa dessa obra é

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Aplicando o Teorema de Pitágoras é possível determinar a

• A.

  medida do volume de um cubo conhecendo-se a medida de sua aresta.

• B.

  medida da área de um retângulo conhecendo-se as medidas de seus lados.

• C.

  distância entre dois pontos quaisquer de uma circunferência conhecendo-se suas coordenadas.

• D.

  constante de proporcionalidade entre duas figuras semelhantes.

• E.

  medida da diagonal de um quadrado conhecendo-se a medida de seu lado e vice-versa.

Ultimamente tem havido muito interesse no aproveita- mento da energia solar para suprir outras fontes de energia. Como exemplo, sabe-se que células solares podem converter a energia solar em energia elétrica e que para cada centímetro quadrado de célula solar que recebe diretamente a luz do sol é gerada 0,01 watt de potência elétrica.

Suponha que a malha quadriculada abaixo apresenta uma fração da superfície retangular do teto de um galpão, parte da qual é revestida por células solares hexagonais, todas feitas de um mesmo material.

Considerando que as dimensões desse teto são 15 m de largura por 16 m de comprimento, então, se a luz do sol incide diretamente sobre tais células, a potência elétrica que elas são capazes de gerar em conjunto é, em watts, igual a

• A.

  160 000.

• B.

  64 000.

• C.

  16 000.

• D.

  6 400.

• E.

  1 600.

Suponha que um recipiente para líquidos seja formado pela junção de um cubo vazado e uma pirâmide (sem a base), cujas faces são triângulos equiláteros, conforme mostrado na figura a seguir.

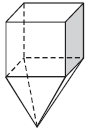
Ao se colocar 158,4 cm ³ de um líquido nesse recipiente, o líquido ocupará o volume da pirâmide, chegando até a metade do volume do cubo. Nesse caso, considerando 1,4 como valor aproximado para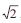, é correto afirmar que a altura ocupada pelo líquido no recipiente, medida desde o vértice da pirâmide até a metade da altura do cubo, será

• A.

  inferior a 2,8 cm.

• B.

  superior a 2,8 cm e inferior a 4,2 cm.

• C.

  superior a 4,2 cm e inferior a 5,6 cm.

• D.

  superior a 5,6 cm e inferior a 6,6 cm.

• E.

  superior a 6,6 cm.

Um lago tem superfície de área 12 km² e 10 m de profundidade média. O volume de água que esse lago comporta é dado pelo produto da área de sua superfície por sua profundidade média. Uma determinada substância está dissolvida nesse lago, de modo que cada metro cúbico de água contém 5 g da substância. Assim sendo, a quantidade total dessa substância no lago é de:

• A.

  6.10⁷ g

• B.

  5.10⁸ g

• C.

  6.10⁸ g

• D.

  5.10⁷ g

Suponha que, na construção de um duto para escoamento da água de um reservatório é usada uma peça feita de alumínio maciço, obtida de um corte de um paralelepípedo retângulo, gerando uma canaleta semicircular, conforme é mostrado na figura abaixo.

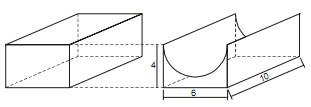
Considerando que as dimensões indicadas na figura são dadas em metros e usando a aproximação π= 3,1, então, se a densidade do alumínio é 2,6 g/cm³, a massa dessa peça em toneladas, é igual a

• A.

  2,613.

• B.

  3,213.

• C.

  26,13.

• D.

  32,13.

• E.

  261,30.

Em uma cooperativa de fruticultores, a comercialização dos produtos de seus associados é decidida em assembleias, em que cada membro tem direito a 1 voto para cada 10.000 árvores plantadas ou fração que possuir. Nesse caso, se N for o número de árvores plantadas que um fruticultor possui e k for o número de votos a que ele tem direito, então

• A.

  

• B.

  

• C.

  

• D.

  

Nessa situação hipotética, considerando-se que um professor de escola particular do estado em questão trabalhe em uma escola cuja carga horária mensal seja de 50 horas e que pague R$ 25,60 por hora-aula, se, em determinado mês, esse professor trabalhar 3 horas após as 22 h, então, de acordo com as instruções acima citadas, o seu salário bruto nesse mês, calculado com duas casas decimais, será de

• A.

  R$ 8.144,64.

• B.

  R$ 6.856,01.

• C.

  R$ 6.936,65.

• D.

  R$ 8.065,61.