Questões de Matemática do ano 2010

É época de copa do mundo e aproveitando o evento um pequeno comerciante investiu R$ 300,00 na produção de bandeiras da Seleção Brasileira. Foram vendidas X bandeiras ao preço de R$ 8,00 cada uma. Então o lucro L(x) obtido na venda de X bandeiras é dado por:

• A.

  L(x) = 8X – 300

• B.

  L(x) = 300 – 8X

• C.

  L(x) = 8X

• D.

  L(x) = 8X + 300

Seja a fração irredutível a geratriz da dízima periódica 0,121212... , um número racional. Então é correto afirmar que:

• A. x + y = 37
• B. x − y = 37
• C. x + y = 111
• D. x − y = 27

Toda a água existente num reservatório R₁ será transferida para outro reservatório R₂, para que sejam feitas as manutenções necessárias. O gráfico a seguir representa o nível de água em cada reservatório em função do tempo, desde o início do processo.

Os níveis de água nos dois reservatórios ficaram iguais, após iniciado o processo, no tempo de

• A. 1 hora e 40 minutos.
• B. 1 hora e 50 minutos.
• C. 2 horas.
• D. 2 horas e 10 minutos.
• E. 2 horas e 20 minutos.

• A.

  40.053.840.

• B.

  40.053,84.

• C.

  400.538,40.

• D.

  4.005.384.

Um agricultor instalou 20 aspersores em uma região retangular cujas dimensões são 40 m e 50 m, de modo a que cada aspersor instalado irrigue uma área circular correspondente a 10 m de diâmetro e que o conjunto de aspersores irrigue a maior área possível.

Nessa situação, considerando 3,14 como valor aproximado de , a área máxima a ser irrigada pelos aspersores, em m2, será igual a

• A.

  1.256.

• B.

  1.570.

• C.

  1.884.

• D.

  2.000.

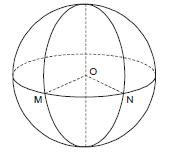
O desenho representa a esfera terrestre em que foram assinalados 2 pontos M e N sobre a linha do equador. Se o ângulo MÔN mede 45°, qual é, em função do raio r da Terra, a medida do arco MN?

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Observe duas circunferências representadas no plano cartesiano. A circunferência C₁ é tangente aos dois eixos em x = 3 e y = 3, enquanto a circunferência C₂ é tangente aos eixos em x = −5 e y = 5.

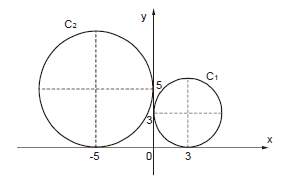
A circunferência C₂ sofrerá uma translação horizontal e uma vertical, de modo que, ao final, seu centro coincidirá com o centro da circunferência C₁. Qual das alternativas contém as translações que a circunferência C₂ executará?

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

• A.

  reflexão na origem.

• B.

  reflexão em torno do eixo x.

• C.

  rotação no sentido anti-horário em torno da origem.

• D.

  rotação no sentido horário em torno da origem.

• E.

  translação em torno da origem.

Em informática, o bit foi criado como um padrão conveniente, para representar a diversidade presente em um conjunto que inclui apenas duas mensagens igualmente prováveis, que podem ser identificadas a partir de uma única pergunta do tipo “sim ou não”. Assim, em um grupo formado por duas mensagens, A e B, que têm as mesmas chances de ocorrência, para identificar qualquer uma delas, escolhida ao acaso, basta uma única pergunta do tipo “sim ou não”; em consequência, diz-se que cada uma delas tem uma quantidade de informação igual a 1 bit. Já em um conjunto mais variado, formado, por exemplo, por 4 mensagens equiprováveis A, B, C, D, é possível identificar uma mensagem escolhida ao acaso, com base em duas perguntas do tipo “sim ou não”. Basta separar o conjunto em duas metades e identificar, com uma pergunta, a parte em que se encontra a mensagem escolhida; recorrendo-se a outra pergunta do mesmo tipo, será possível descobrir exatamente a mensagem referida. Nesse caso, diz-se que cada uma das mensagens tem 2 bits de informação. Raciocinando-se de modo semelhante, conclui-se que, em um repertório de 8 mensagens, a quantidade de informação de cada uma delas é igual a 3 bits; se forem 16 as mensagens equiprováveis, cada uma terá 4 bits, e assim por diante.

Embora o número n de mensagens não seja, necessariamente, igual a uma potência inteira de 2, ainda assim é possível medir a quantidade k de informação, em bits, procurando-se o número k tal que

• A.

  k = 2n.

• B.

  2^k = n.

• C.

  k = 2n + 1.

• D.

  2ⁿ = k.

Considere as seguintes afirmações:

I. Se x é um número inteiro, então .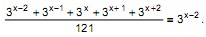

II. 0,36363612480215 . . . é um número racional.

III. A expressão (8,8 X 10^-9). (6,025 X 10⁶) é equivalente a 5,305 X 10^-2.

Relativamente a essas afirmações, é correto afirmar que

• A.

  I, II e III são verdadeiras.

• B.

  apenas I e III são verdadeiras.

• C.

  apenas II e III são verdadeiras.

• D.

  apenas uma é verdadeira.

• E.

  I, II e III são falsas.