Questões de Matemática do ano 2010

Se 4 homens embrulham 88 ovos de páscoa em 20 minutos e 3 mulheres embrulham 150 ovos de páscoa em 25 minutos, quantos ovos de páscoa são embrulhados por 3 homens e 2 mulheres em 30 minutos?

• A.

  119.

• B.

  219.

• C.

  230.

• D.

  188.

Sabe-se que enchendo 84 garrafas, cada uma com capacidade de 0,80 ℓ, é possível engarrafar todo o líquido de um reservatório. Se o volume de cada garrafa fosse 896 cm³, o número de garrafas utilizadas seria, aproximadamente:

• A.

  75.

• B.

  700.

• C.

  70.

• D.

  750.

Um número real é tal que a sua quarta potência é igual a 5 somando com o quádruplo do seu quadrado. Determine esse número.

• A.

  {-1;5}.

• B.

  {25;1}.

• C.

  

• D.

  {1;-5}.

Texto para as questões 15 e 16

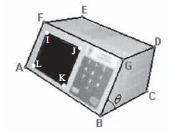
A figura acima ilustra a eletrônica usada nas últimas eleições no Brasil. Ela contém um painel frontal retangular, ABGF, com inclinação θ = 45º em relação à base ABCH — o vértice H, que não aparece explicitamente na figura, é comum às faces ABCH, CDEH e AFEH. As faces BCDG e AFEH são paralelas entre si e são trapézios retângulos; todas as outras faces são retângulos. O retângulo IJKL, correspondente ao monitor de vídeo, tem dimensões IJ = 20 cm e JK = 15 cm; a distância do segmento KL ao segmento AB é igual a 2 cm e a distância do segmento IJ ao segmento FG é igual a 3 cm.

Caso se resolva aumentar as dimensões da urna eletrônica, de modo que o monitor de vídeo da nova urna seja semelhante ao da mostrada na figura e o comprimento do lado maior do novo monitor seja igual a 24 cm, então a razão entre a área do novo monitor e a do antigo será igual a

• A.

  

• B.

  

• C.

  1.

• D.

  

• E.

  

Considere a seguinte sucessão de igualdades:

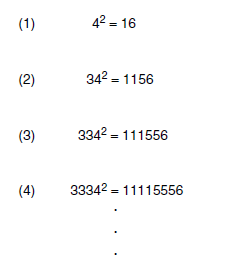
Considerando que, em cada igualdade, os algarismos que compõem os números dados obedecem a determinado padrão, é correto afirmar que a soma dos algarismos do número que apareceria no segundo membro da linha (15) é um número:

• A.

  quadrado perfeito.

• B.

  maior que 100.

• C.

  divisível por 6.

• D.

  par.

• E.

  múltiplo de 7.

Certo dia, Valfredo saiu de casa em direção ao trabalho quando seu relógio digital de pulso marcava 9 horas, 15 minutos e 56 segundos, conforme mostra o esquema abaixo.

Se Valfredo chegou ao trabalho no instante em que todos os números que apareciam no mostrador do seu relógio mudaram simultaneamente pela primeira vez, então, nesse dia, o tempo que ele levou para ir de casa ao trabalho foi de

• A.

  38 minutos e 12 segundos.

• B.

  38 minutos e 52 segundos.

• C.

  42 minutos e 24 segundos.

• D.

  44 minutos e 4 segundos.

• E.

  44 minutos e 36 segundos.

Seja XYZ um número inteiro e positivo em que X, Y e Z representam os algarismos das centenas, das dezenas e das unidades, respectivamente. Sabendo que 36 935 ÷ (XYZ) = 83, é correto afirmar que

• A.

  X = Z

• B.

  X . Y = 16

• C.

  Z − Y = 2X

• D.

  Y = 2X

• E.

  Z = X + 2

Existe uma regra prática de divisibilidade por 7 com o seguinte procedimento:

Separa-se o último algarismo da direita. Multiplica-se esse algarismo por 2 e tal resultado é subtraído do número que restou sem o algarismo à direita. Procede-se assim, sucessivamente, até se ficar com um número múltiplo de 7, mesmo que seja zero.

Veja os exemplos a seguir:

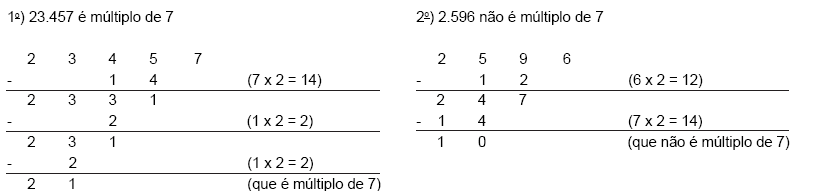
 Seja a um algarismo no número a13.477.307. O valor de a para que este número seja divisível por 7 é

• A.

  1

• B.

  3

• C.

  5

• D.

  7

• E.

  9

Um homem entra numa livraria, compra um livro que custa 20 reais e paga com uma nota de 100 reais. Sem troco, o livreiro vai até a banca de jornais e troca a nota de 100 por 10 notas de 10 reais. O comprador leva o livro e 8 notas de 10 reais. Em seguida, entra o jornaleiro dizendo que a nota de 100 reais é falsa. O livreiro troca a nota falsa por outra de 100, verdadeira. O prejuízo do livreiro, em reais, sem contar o valor do livro, foi

• A.

  200

• B.

  180

• C.

  100

• D.

  80

• E.

  20

Considerando-se N um número inteiro e positivo, analise as afirmações seguintes, qualquer que seja o valor de N:

I - N² + N + 1 é um número ímpar;

II - N⋅ (N + 1) ⋅ (N + 2) é um número múltiplo de 3;

III - N² tem uma quantidade par de divisores;

IV - N + (N + 1) + (N + 2) é um número múltiplo de 6.

 A quantidade de afirmações verdadeiras é

• A.

  1

• B.

  2

• C.

  3

• D.

  4

• E.

  0