Questões de Matemática do ano 2010

Um quadrado é cortado em 17 quadrados menores. Todos esses quadrados têm as medidas de seus lados, em centímetros, expressas por números inteiros positivos. Há exatamente 16 quadrados com área igual a 1 cm². A área do quadrado original, em cm², vale

• A.

  81

• B.

  64

• C.

  49

• D.

  36

• E.

  25

Se os cientistas desenrolarem e unirem todos os cordões do DNA contidos em uma célula o tamanho total chegaria a 186 cm. Sabe-se que um ser humano possui em torno de 100 trilhões de células. Qual o comprimento de todos os cordões unidos contidos nas células de um ser humano?

• A.

  1,86 . 10¹¹ km.

• B.

  1,86 . 10¹³ km.

• C.

  1,86 . 10¹⁵ km.

• D.

  1,86 . 10¹⁶ km.

• E.

  1,86 . 10 ¹⁷ km.

O fabricante de um automóvel tipo X anuncia que o veículo apresenta a relação de consumo de 15 km por litro de gasolina, se desenvolver velocidade na faixa de 60 a 80 km/h. Se a velocidade exceder essa faixa, o consumo de combustível aumenta em 20%. Quantos litros de gasolina serão consumidos por esse automóvel em um percurso de 540 km, se a primeira metade for cumprida com valor de velocidade dentro da faixa recomendada, e o restante com valor acima da faixa?

• A.

  32,0 litros.

• B.

  33,0 litros.

• C.

  33,7 litros.

• D.

  39,6 litros.

• E.

  40,5 litros.

Gauss ou Johann Carl Friedrich Gauss foi um matemático, astrônomo e físico alemão. Conhecido como o príncipe dos matemáticos e considerado por muitos o maior gênio da matemática. Mostrou sua genialidade desde cedo. Conta-se que por volta dos dez anos de idade surpreendeu o professor na sala de aula. Para somar de 1 a 100, Gauss percebeu que era muito mais fácil efetuar a adição, não na ordem em que os números foram apresentados e sim das extremidades para o meio, somando os pares equidistantes dos extremos.

Ele encontrou como resultado

• A.

  505

• B.

  5 050

• C.

  50 050

• D.

  50 500

• E.

  10 100

Para calcular o valor numérico de uma expressão algébrica podemos, inicialmente, simplificá-la a fim de reduzir o número de operações. Por exemplo, na expressão

• A.

  4,25.

• B.

  3,75.

• C.

  2,25.

• D.

  1,95.

• E.

  1,20.

Um pesquisador entrevistou 500 alunos ingressantes de uma universidade a fim de saber em qual escola haviam concluído o Ensino Médio, com os seguintes resultados:

É correto afirmar que

• A.

  Beta tem um número maior de ingressantes do que todas as outras escolas juntas.

• B.

  o percentual menor de alunos ingressantes pertence somente à escola Gama.

• C.

  a escola Beta teve o maior percentual de ingressantes de todas as escolas pesquisadas.

• D.

  a escola Alfa tem um terço do percentual de ingressantes que as escolas Gama e Beta juntas.

• E.

  a escola Ômega tem um quarto do percentual de ingressantes que todas as outras juntas.

Dois números racionais não nulos são inversos entre si quando o produto entre eles resulta no elemento neutro da multiplicação, ou seja, resulta 1. Assim, por exemplo, 0,8 e 1,25 são inversos entre si, pois 0,8 × 1,25 = 1,0. Existe um número real que quando adicionado ao numerador e subtraído do denominador da fração 7 /13 faz com que ela se converta em sua inversa. Esse número é

• A.

  um quadrado perfeito, como 4, por exemplo, que é o quadrado de 2.

• B.

  primo, ou seja, só é divisível por 1 e por si mesmo.

• C.

  decimal não exato, como 1,2 ou 3,51, por exemplo.

• D.

  um dos divisores de 24, como 2 ou 3, por exemplo.

• E.

  inteiro negativo, como −5, por exemplo.

Quantos copos com 200 mL de água, no mínimo, são necessários para encher completamente o vasilhame cônico representado na figura?

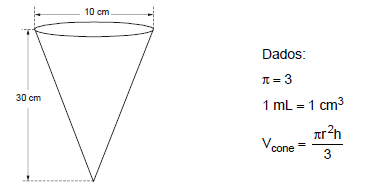
• A.

  4 copos.

• B.

  5 copos.

• C.

  12 copos.

• D.

  15 copos.

• E.

  16 copos.

Observe a tabela contendo valores de algumas potências de base 3.

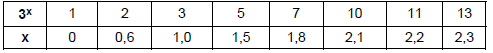
Com base nos valores dessa tabela, qual é a solução da equação 3^x = 150?

• A.

  4,6.

• B.

  4,5.

• C.

  4,4.

• D.

  4,3.

• E.

  4,2.

A receita diária de uma locadora de DVDs é dada por R = 5 p² − 80 p, em que p é o preço cobrado por vídeo alugado. Qual deve ser o valor mínimo cobrado por DVD alugado para que a receita diária seja de R$ 180,00?

• A.

  R$ 4,00.

• B.

  R$ 6,00.

• C.

  R$ 8,00.

• D.

  R$ 10,00.

• E.

  R$ 12,00.