Questões de Matemática do ano 2013

Na cidade onde Adriano mora, os táxis cobram uma quantia fixa de R$4,20 mais R$0,65 por quilômetro rodado. Quando Adriano pega um taxi e faz um percurso de 12km, o valor pago pela corrida é igual a

• A.

  R$7,80

• B.

  R$9,20.

• C.

  R$12,00

• D.

  R$13,80

• E.

  R$14,00.

Uma empresa pode vender 1000 unidades de um determinado produto pelo preço unitário de R$30,00 e, se o preço unitário desse mesmo produto for R$25,00, ela poderá vender 2000 unidades. Considerando que a quantidade vendida (q) pode ser expressa em função do preço unitário (p) por uma função afim, a expressão que melhor representa essa situação é:

• A.

  q( p) = −7000 p + 200

• B.

  q( p) = 200 p + 7000

• C.

  q( p) = −200 p + 7000

• D.

  q( p) = 7000 p − 200

• E.

  q( p) = 200 p − 7000

• A.

  1600 J

• B.

  900 J

• C.

  700 J

• D.

  630 J

• E.

  200 J

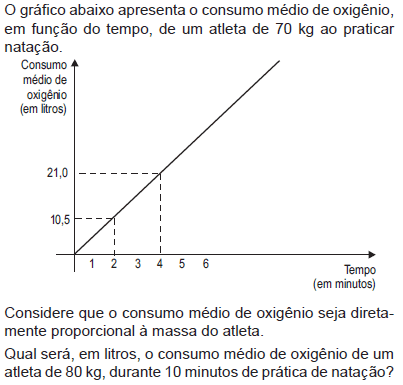
• A.

  50,0

• B.

  52,5

• C.

  55,0

• D.

  57,5

• E.

  60,0

Se um cliente, ao usufruir do pacote de serviços, pagou, para ele e para sua esposa, a quantia de R$ 300,00 de taxa de uso, por três dias de estadia em um hotel da rede, então, para passar os quatro dias restantes com a esposa e com dois filhos no mesmo hotel, o cliente pagará

• A.

  R$ 800,00.

• B.

  R$ 900,00.

• C.

  R$ 1.200,00.

• D.

  R$ 400,00.

• E.

  R$ 600,00.

Um Agente Administrativo realizou um levantamento sobre a quantidade de ofícios enviada a repartições públicas, durante um dia de trabalho. Foi constatado que esse número corresponde ao conjunto solução da equação exponencial  Nessas condições, a quantidade de ofícios enviada é igual a

• A.

  2

• B.

  5

• C.

  8

• D.

  11

• E.

  14

O montante de uma aplicação financeira no decorrer dos anos é dado por M(t) = 900 × (1,03)^t , onde t representa o mês após a aplicação, e t=0 o momento em que foi realizada a aplicação. Para obtermos um montante de R$1.800,00, o tempo de aplicação deve ser de (use log₂ (1,03)= 0,04 )

• A.

  15 meses.

• B.

  18 meses.

• C.

  20 meses.

• D.

  23 meses.

• E.

  25 meses.

Se 5ⁿ + 5^-n = 10 , o valor de 25ⁿ + 25^-n é

• A.

  100.

• B.

  98.

• C.

  75.

• D.

  50.

• E.

  68.

Em um terreno plano, uma formiga encontra-se, inicialmente, no centro de um quadrado cujos lados medem 2 metros. Ela caminha, em linha reta, até um dos vértices (cantos) do quadrado. Em seguida, a formiga gira 90 graus e recomeça a caminhar, também em linha reta, até percorrer o dobro da distância que havia percorrido no primeiro movimento, parando no ponto P. Se V é o vértice do quadrado que se encontra mais próximo do ponto P, então a distância, em metros, entre os pontos P e V é

• A.

  igual a 1.

• B.

  um número entre 1 e 2.

• C.

  igual a 2.

• D.

  um número entre 2 e 4.

• E.

  igual a 4.

As seis faces de um dado são quadrados cujos lados medem L. A distância do centro de um desses quadrados até qualquer um de seus vértices (cantos do quadrado) é igual a D. Uma formiga, que se encontra no centro de uma das faces do dado, pretende se deslocar, andando sobre a superfície do dado, até o centro da face oposta. A menor distância que a formiga poderá percorrer nesse trajeto é igual a

• A.

  2L.

• B.

  2L + D.

• C.

  2L + 2D.

• D.

  L + 2D.

• E.

  L.