Questões sobre Aritmética e Algebra

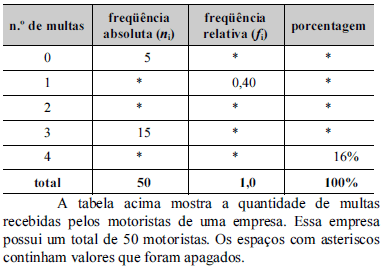
Com base nessas informações, julgue os itens que se seguem.

O total de multas recebidas pelos motoristas da empresa foi inferior a 100.

• C. Certo
• E. Errado

Julgue os itens seguintes.

A interseção entre o conjunto dos múltiplos positivos de 6 e o conjunto dos divisores positivos de 60 tem 3 elementos.

• C. Certo
• E. Errado

Os hindus, a partir do século VI, efetuavam multiplicações por um método denominado "por quadriculagem". VamosA seguir, adicionam-se os algarismos compreendidos entre as diagonais, da esquerda para a direita e de cima para baixo, colocando-se os resultados no exterior do retângulo maior. Obtém-se, dessa forma, que o resultado de 532 × 75 é 39 900.O quadro seguinte, mostra a multiplicação entre dois números de dois algarismos:O produto obtido nessa multiplicação é igual a mostrá-lo, multiplicando 532 por 75. Para tal, desenhamos um retângulo composto por 6 outros retângulos, dispostos em três colunas (número de algarismos de 532) e duas linhas (número de algarismos de 75). Cada retângulo, dividido pela sua diagonal, traz em cada metade um algarismo do número resultante da multiplicação do algarismo da linha pelo da coluna.

A seguir, adicionam-se os algarismos compreendidos entre as diagonais, da esquerda para a direita e de cima para baixo, colocando-se os resultados no exterior do retângulo maior. Obtém-se, dessa forma, que o resultado de 532 x 75 é 39 900

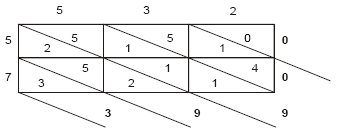
O quadro seguinte, mostra a multiplicação entre dois números de dois algarismos:

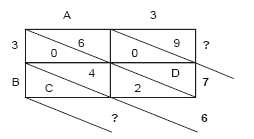
O produto obtido nessa multiplicação é igual a

• A.

  1 679

• B.

  1 426

• C.

  689

• D.

  649

• E.

  619

Dois amigos têm, cada um, mais de 50 anos de idade e menos de 56 anos. Fatorando-se essas idades, verifica-se que cada uma tem apenas 2 fatores primos e que esses 4 fatores são todos distintos. Considerando esses 4 números primos, julgue os itens subseqüentes.

A soma dessas idades é superior a 105.

• C. Certo
• E. Errado

Uma mercearia vende dois tipos de farinha: a farinha A, que custa R$ 0,95 por kg, e a farinha B, que custa R$ 1,15 por kg. Misturando apenas os dois tipos de farinha, o comerciante deseja obter 60 kg de uma mistura de farinhas ao preço de R$ 1,00 o quilograma. Com base nessas informações, julgue os itens subseqüentes.

Para atingir o seu objetivo, a quantidade de farinha A que o comerciante deve colocar na mistura é superior a 40 kg.

• C. Certo
• E. Errado

Leia as afirmações abaixo.

I. A avaliação mediante testes e exames diz muito pouco sobre aprendizagem. Na verdade, os alunos passam em testes para os quais são treinados. É essencial distinguir educação de treinamento.

II. Não conhecer um determinado assunto, seja por falta de interesse, seja por falta de capacidade para aprender esse tema, é grave.

III. O docente está num processo permanente de aprimorar sua prática e nada melhor para isso do que ele próprio conhecer seu desempenho por meio de relatórios dessa prática, feitos pelos alunos.

As afirmações que estão em desacordo com a proposta de avaliação defendida por Ubiratan D'Ambrosio, em seu livro Educação Matemática: da teoria à prática são, APENAS,

• A.

  I e II.

• B.

  II e III.

• C.

  I e III.

• D.

  II.

• E.

  III.

Dois amigos têm, cada um, mais de 50 anos de idade e menos de 56 anos. Fatorando-se essas idades, verifica-se que cada uma tem apenas 2 fatores primos e que esses 4 fatores são todos distintos. Considerando esses 4 números primos, julgue os itens subseqüentes.

O produto entre o menor e o maior número primo é inferior a 50.

• C. Certo
• E. Errado

Uma mercearia vende dois tipos de farinha: a farinha A, que custa R$ 0,95 por kg, e a farinha B, que custa R$ 1,15 por kg. Misturando apenas os dois tipos de farinha, o comerciante deseja obter 60 kg de uma mistura de farinhas ao preço de R$ 1,00 o quilograma. Com base nessas informações, julgue os itens subseqüentes.

Para atingir o seu objetivo, a quantidade de farinha A que o comerciante deve colocar na mistura é superior a 40 kg.

• C. Certo
• E. Errado

No século IX o matemático Al-Jawhari desenvolveu métodos de resolução de equações, incluindo processos geométricos. Vamos ver um exemplo de representação geométrica para a resolução de uma equação de segundo grau em x. Traçam-se primeiramente um quadrado de lado x unidades e quatro retângulos de lados 2,5 e x unidades.

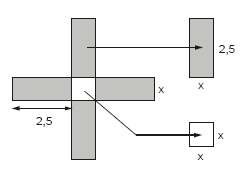
Em seguida, acrescentam-se quatro quadrados de lado 2,5 unidade, obtendo-se dessa forma um quadrado de lado (2,5 + 2,5 + x)

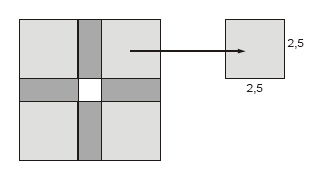
Se esse quadrado tem área de 64 unidades quadradas, o valor de x e uma possível equação para essa representação são

• A.

  4 e x² + 10x = 56

• B.

  4 e x² + 12x = 64

• C.

  3 e 3x² − 55x = 64

• D.

  3 e x² + 10x = 39

• E.

  3 e x² + 8x = −33

Dois amigos têm, cada um, mais de 50 anos de idade e menos de 56 anos. Fatorando-se essas idades, verifica-se que cada uma tem apenas 2 fatores primos e que esses 4 fatores são todos distintos. Considerando esses 4 números primos, julgue os itens subseqüentes.

A soma dos dois números primos maiores é superior a 25.

• C. Certo
• E. Errado