Questões sobre Aritmética e Algebra

No estacionamento de um shopping center, o garagista notou que cada veículo que chegava tinha uma quilometragem 10 km superior à quilometragem do veículo anterior, e que o hodômetro do 1.º veículo que chegou marcava exatamente 20 km. Considerando que entraram 40 veículos no estacionamento, julgue os itens que se seguem.

A quilometragem do 25.º veículo é exatamente o dobro da quilometragem do 12.º veículo.

• C. Certo
• E. Errado

Considere o texto apresentado abaixo para responder as questões de números 27 e 28.

Segundo a autora, a análise da resolução de Dony mostra que:

• A.

  é fundamental que as maneiras convencionais de resolução de problemas, utilizando uma adição ou uma subtração, sejam apresentadas às crianças desde o início do trabalho.

• B.

  encontrar uma estratégia adequada para resolver um problema é algo muito diferente de poder representá- lo através de uma conta convencional.

• C.

  a utilização de algoritmos tradicionais, de adições e/ou subtrações, estimula nas crianças o desejo de diminuir o tempo despendido na resolução de algum problema.

• D.

  na resolução de problemas envolvendo somas e subtrações as crianças utilizam estratégias mentais primárias, que podem ser substituídas, com sucesso, por técnicas convencionais.

• E.

  a maneira mais eficiente de resolver determinado problema sempre exigirá a utilização de um algoritmo convencional.

H. O. Pollack, no livro Aplicações da matemática escolar, trabalho conjunto da Associação Matemática da América, publicado pela Editora Atual, diz, sobre a utilização de modelos matemáticos: Deve-se lembrar também que os modelos matemáticos têm uma multiplicidade de propósitos. Estes vão desde uma compreensão melhor da situação original até a ação decorrente de um resultado da análise. O grau de precisão que se espera de um modelo matemático também varia consideravelmente. As situações da engenharia e da física podem freqüentemente ser modeladas com muita precisão; as situações das ciências sociais podem não se prestar à mesma precisão matemática Não obstante, tais modelos matemáticos não são necessariamente menos importantes ou decisivos enquanto instrumento que proporciona a compreensão e serve de base para a ação.

Com base no texto, é correto o que se afirma em:

• A.

  Os modelos matemáticos têm importância diminuída em ciências sociais porque não apresentam precisão.

• B.

  O propósito de qualquer modelo matemático é único: o de resolver uma situação-problema.

• C.

  Modelos matemáticos podem servir para uma melhor compreensão da situação original.

• D.

  É suficiente a determinação correta das variáveis envolvidas numa situação-problema para uma boa realização de modelos matemáticos.

• E.

  Modelos matemáticos só podem ser utilizados nas ciências exatas e da natureza.

Um juiz deve julgar 52 processos, que estão separados, por assunto, em 3 grupos. Sabe-se que o máximo divisor comum (MDC) e o mínimo múltiplo comum (MMC) entre os números de processos em cada um dos grupos são 4 e 48, respectivamente. Acerca desses grupos de processos, julgue os itens seguintes.

Um dos grupos contém mais processos que os outros dois juntos.

• C. Certo
• E. Errado

Uma empresa adquiriu uma impressora de médio porte e dois computadores por R$ 18.000,00. Em uma segunda compra, no valor de R$ 42.000,00, o fornecedor manteve os preços dos produtos e a empresa duplicou o número de impressoras e triplicou o de computadores. A respeito dessa negociação, julgue os itens subseqüentes.

Com a quantia gasta na compra de duas impressoras, seria possível comprar mais de sete computadores.

• C. Certo
• E. Errado

Para representar um número natural qualquer podemos utilizar a letra n. Para representar um número natural ímpar qualquer podemos utilizar a notação 2n + 1. Sendo assim, o resultado de (2n + 1)² sempre será, para qualquer n, um número

• A.

  primo.

• B.

  múltiplo de 3.

• C.

  par.

• D.

  ímpar

• E.

  divisor de 72.

Os pitagóricos, na primeira metade do século VI a.C., segundo Boyer, em seu livro História da Matemática, estudaram os números e os classificaram de acordo com propriedades bem definidas. Assim, denominaram como perfeito o número natural cuja soma de seus divisores, distintos dele mesmo, é igual a ele.

 28 é perfeito porque 28 = 1 + 2 + 4 + 7 + 14

Nicómano, no século II a.C enunciou a seguinte propriedade, relativa aos números perfeitos: se a soma 2⁰+2 +2² +2³ +...+ 2ⁿ = p é um número primo, então 2ⁿ x p é perfeito. Baseado nesta fórmula, o número perfeito e o valor correspondente de p são, respectivamente,

• A.

  256 e p = 13

• B.

  496 e p =31

• C.

  812 e p = 29

• D.

  7116 e p = 593

• E.

  8120 e p =203

Um juiz deve julgar 52 processos, que estão separados, por assunto, em 3 grupos. Sabe-se que o máximo divisor comum (MDC) e o mínimo múltiplo comum (MMC) entre os números de processos em cada um dos grupos são 4 e 48, respectivamente. Acerca desses grupos de processos, julgue os itens seguintes.

Dois dos grupos contêm, juntos, 36 processos.

• C. Certo
• E. Errado

Julgue os itens que se seguem, acerca da aplicação de razões e proporções e de equações.

Considere que, para construir um reservatório, 30 homens trabalharam durante 18 dias e, em seguida, 36 homens trabalharam durante 12 dias. Considerando ainda que os homens produzam a mesma quantidade de serviço por dia de trabalho, se 36 homens tivessem trabalhado ininterruptamente, é correto afirmar que a obra teria ficado pronta em menos de 25 dias.

• C. Certo
• E. Errado

Um problema clássico consiste em calcular valores de x de modo que 10^x tenha resultados iguais a 1, 2, 3, 4, 5, 6, etc, com boa aproximação.

O valor de x em 10^x=1 é x= 0, pois 10⁰ = 1

Para calcular o valor de x em 10^x = 2, adotaremos a seguinte estratégia: vamos escrever potências de 10 e potências de 2 e procurar, dentre elas, os valores mais próximos.

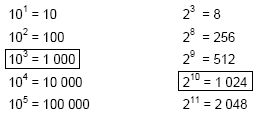
Aproximando 1000 para 1024, teremos:

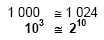
Extraíndo a raiz décima de ambos os membros, ficaremos com o seguinte:

Com base nesse procedimento e considerando a aproximação entre 2 x 10⁴ = 20 000 e 3⁹ = 19 683, o valor de x para 10^x = 3 é

• A.

  0,330

• B.

  0,410

• C.

  0,478

• D.

  0,555

• E.

  0,984