Questões sobre Aritmética e Algebra

Quantos gramas há em 3 (três) toneladas?

• A.

  300.000 gramas.

• B.

  3.000.000 gramas.

• C.

  30.000 gramas.

• D.

  3.000 gramas.

A autora Delia Lerner de Zunino, em seu livro A matemática na escola: aqui e agora, critica a inconveniência de uma conhecida concepção de ensino e aprendizagem em Matemática. Em qual das afirmações NÃO são apontadas características da concepção criticada pela autora?

• A.

  Ensinar consiste em explicar, aprender consiste em repetir o ensinado até reproduzi-lo fielmente.

• B.

  Ensinar consiste em utilizar muito material concreto e exercitar muito... repetir muitas vezes.

• C.

  As crianças, de modo geral, não são capazes de aprender muitas coisas a partir de sua experiência familiar e social.

• D.

  Os conhecimentos devem ser separados cuidadosamente, para evitar confusões, desse modo as crianças poderão aprender de forma organizada.

• E.

  Ensinar consiste em reconhecer que a aprendizagem de certos conteúdos começa antes do ingresso da criança na escola.

Ao devolver a prova corrigida para a classe, o professor comentou:

 − Pessoal, nessa prova, que valia de 0 a 10, as meninas foram melhor que os meninos, pois a nota média das meninas foi igual a 6,2 enquanto a nota média dos meninos foi igual a 5,9.

A partir da fala do professor, pode-se afirmar que

• A.

  a maioria das meninas tirou nota acima de 6,0.

• B.

  há mais meninas que meninos nessa classe.

• C.

  que todas as meninas podem ter tirado nota igual a 6,2.

• D.

  dentre as meninas a nota mais freqüente foi 6,2.

• E.

  a soma das notas de todos os meninos é menor que a soma das notas de todas as meninas.

Em seu livro Matemática e língua materna, o autor Nilson José Machado, expõe, já na introdução, uma das linhas de raciocínio de abordagem de seu texto, quando escreve:

Um dos objetivos do autor, nesta obra, é mostrar que:

• A.

  entre a Matemática e a Língua Materna existe, ou deveria existir, uma complementaridade nas metas que perseguem, um paralelismo nas funções que desempenham nos currículos.

• B.

  a capacidade para a Matemática é inata enquanto a capacidade para a leitura e escrita pode ser desenvolvida igualmente em todos os indivíduos.

• C.

  a matemática, ensinada apenas como uma linguagem, aproxima-se da língua portuguesa, na qual as regras gramaticais ocupam o centro das atenções.

• D.

  a Matemática, diferentemente da Língua Materna, o Português, é exata, abstrata e desenvolve o raciocínio.

• E.

  a matemática justifica-se pelas aplicações práticas, contrariamente à Língua Materna, como é possível perceber da citação de Lobachvsky: Não há ramo da Matemática, por abstrato que seja, que não possa um dia vir a ser aplicado aos fenômenos do mundo real.

Julgue os itens que se seguem.

Considere que o fogão da casa de Joana consuma dois botijões de gás de cozinha de 13 kg a cada 3 meses, que um botijão de gás de 13 kg custa R$ 22,50 e que o salário mensal de Joana é de R$ 240,00. Nessas condições, é correto concluir que Joana gasta menos de 6/100 do seu salário na compra de gás de cozinha.

• C. Certo
• E. Errado

O triângulo seguinte aparece num livro chinês chamado O precioso Espelho dos Quatro Elementos, escrito por Chu Shih Chieh em 1303. Cada símbolo diferente corresponde a um número do nosso sistema de numeração. Obser-vando as linhas do triângulo é possível descobrir uma forma matemática de obtenção dos números de uma linha a partir dos números da linha anterior. Desse modo, é possível construir tantas linhas quantas se quiser no triângulo.

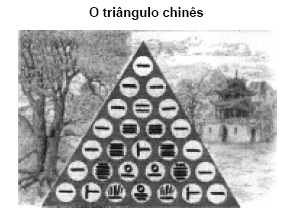
Considerando a seqüência mostrada nas linhas do triângulo, os números do sistema decimal de numeração que corresponderiam, respectivamente, aos símbolos da oitava linha são

• A.

  1, 6, 15, 20, 15, 6, 1

• B.

  1, 7, 21, 35, 35, 21, 7, 1

• C.

  1, 7, 14, 28, 28, 14, 7, 1

• D.

  1, 8, 24, 40, 56, 40, 24, 8, 1

• E.

  1, 8, 29, 56, 70, 56, 29, 8, 1

Julgue os itens que se seguem.

Considere a seguinte situação hipotética.

O prédio da prefeitura de uma cidade possui 12 salas do tipo I, 15 salas do tipo II e 20 salas do tipo III. O prefeito da cidade decidiu instalar lâmpadas em todas as salas de modo que apenas salas de um mesmo tipo tenham o mesmo número de lâmpadas.

Nessa situação, serão necessárias mais de 80 lâmpadas para o prefeito realizar o seu projeto.

• C. Certo
• E. Errado

Conhecimentos prévios são todos aqueles comportamentos (corretos ou incorretos) que cada sujeito possui e que adquiriu ao longo de sua vida na interação com o mundo que o cerca e com a escola. (POZO Juan Ignacio, em A solução de problemas)

Nas afirmações seguintes são apresentadas características, algumas corretas outras incorretas, dos chamados conhecimentos prévios.

I. São construções pessoais dos alunos.

II. São cientificamente coerentes.

III. Procuram mais a utilidade do que a verdade.

IV. São facilmente verbalizados por todos os alunos.

V. São, geralmente, estáveis e resistentes à mudança.

As características corretas são APENAS aquelas identificadas com as afirmações

• A.

  I, III e V.

• B.

  I, II, III e IV.

• C.

  I, III e IV.

• D.

  II, III e V.

• E.

  I, II e IV.

Leia o trecho retirado do livro A solução de problemas de Juan Ignácio Pozo:

Qual, dentre os seguintes termos, é a denominação correta para a reflexão sobre o próprio conhecimento, de que fala o autor?

• A.

  Memorização.

• B.

  Metacognição.

• C.

  Transposição didática.

• D.

  Adaptação cognitiva.

• E.

  Desenvolvimento de competências.

Na quinta noite de sonhos, Robert, o menino personagem do livro O diabo dos números, de Hans Manus Enzensberger, conheceu os números quadrangulares e triangulares e algumas de suas propriedades. O número 36, por exemplo, é simultaneamente quadrangular e triangular, como mostram as representações abaixo.

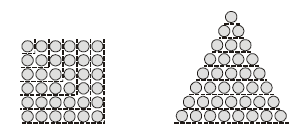
Na seqüência dos números triangulares, 1, 3, 6, 10, ... o 12.º número é

• A.

  76

• B.

  78

• C.

  ímpar.

• D.

  quadrangular.

• E.

  divisível por 4.