Questões sobre Coordenadas cartesianas
Lista completa de Questões sobre Coordenadas cartesianas para resolução totalmente grátis. Selecione os assuntos no filtro de questões e comece a resolver exercícios.
Matemática - Coordenadas cartesianas - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2012
Texto para as questões 30 e 31
Ao executar um salto de paraquedas, a curva descrita pelo paraquedista, em um sistema tridimensional de coordenadas cartesianas ortogonais xyz, é expressa por α(t) = (x(t), y(t), z(t)) em que x(t) = sen6t, y(t) = cos6t e z(t) = !8t + 4.000, em que t representa o tempo, em segundos, a partir do momento do salto, que ocorreu em t = 0. As distâncias x(t), y(t) e a altura z(t) são expressas em metros.
- A.
(0, 2, 1)
- B.
(1, 3, 4)
- C.
(1, 0, 2)
- D.
(4, 1, 3)
- E.
(0, !6, !8)
- A.
100
- B.
160
- C.
440
- D.
560
- E.
880
- A.
nulo.
- B.
decimal periódico.
- C.
positivo.
- D.
inteiro negativo.
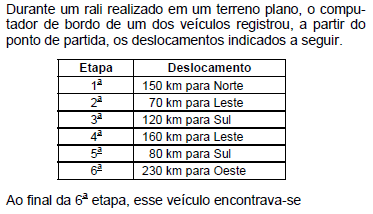
- A.
100 km ao Sul do ponto de partida.
- B.
100 km ao Norte do ponto de partida.
- C.
50 km ao Sul do ponto de partida.
- D.
50 km ao Norte do ponto de partida.
- E.
30 km a Oeste do ponto de partida.
O rumo da linha 1-3 é:
- A.
70º NE
- B.
16º NE
- C.
16º SW
- D.
20º SW
- E.
20º NE
Um rapaz e uma moça estão juntos no centro de um campo de futebol. Andam um metro juntos na direção NORTE. A partir desse ponto a moça para de andar e fica olhando fixamente para a direção NORTE. O rapaz gira 90° e anda 2 metros na direção OESTE; gira novamente 90° e anda 4 metros na direção SUL; gira 90° e anda 8 metros na direção LESTE; gira 90° e anda 16 metros na direção NORTE; gira 90° e anda 32 metros na direção OESTE e para. A distância, em metros, entre o rapaz e a moça quando ele cruza a linha imaginária do olhar da moça é, a partir desses dados,
- A.
32.
- B.
24.
- C.
19.
- D.
16.
- E.
12.
Matemática - Coordenadas cartesianas - Fundação para o Vestibular da Universidade Estadual Paulista (VUNESP) - 2012
- A.
2
- B.
- C.
- D.
- E.
Matemática - Coordenadas cartesianas - Fundação para o Vestibular da Universidade Estadual Paulista (VUNESP) - 2012
- A.
do Teorema de Tales para o ponto médio e do Teorema de Pitágoras para a distância.
- B.
do Teorema de Pitágoras para o ponto médio e da congruência de triângulos para a distância.
- C.
da congruência de triângulos para os dois casos.
- D.
do Teorema de Pitágoras para os dois casos.
- E.
do Teorema de Tales para os dois casos.
Sendo o triângulo cujos vértices possuem as coordenadas A (1; 2), B (3; 4) e C (4; -1), e sendo p a sua área. Então 3/2 p, é?
- A.
8.
- B.
12.
- C.
9.
- D.
15.
- E.
6.
Matemática - Coordenadas cartesianas - Fundação Professor Carlos Augusto Bittencourt (FUNCAB) - 2012
Determine o valor de y, quando x = 2, na função y = ax² + bx + c, cujo gráfico passa pelos pontos (-1, 0), (5, 0) e (1, -8).
- A.
y = - 2
- B.
y = - 6
- C.
y = - 3/2
- D.
y = - 9
- E.
y = 0
O Provas e Concursos é um banco de dados de questões de concursos públicos organizadas por matéria, assunto, ano, banca organizadora, etc
