Questões sobre Derivadas
Lista completa de Questões sobre Derivadas para resolução totalmente grátis. Selecione os assuntos no filtro de questões e comece a resolver exercícios.
A função 
possui um ponto crítico em t 0 . Considerando 1,6 como valor aproximado de ln 5, então t 0 é igual a
- A.
2
- B.
5
- C.
10
- D.
15
- E.
20
Com relação a esse movimento, julgue os seguintes itens.
A curva que descreve o movimento da partícula é sempre crescente.
- C. Certo
- E. Errado
Com relação a esse movimento, julgue os seguintes itens.
A curva que descreve o movimento da partícula é côncava para cima.
- C. Certo
- E. Errado
Com relação a esse movimento, julgue os seguintes itens.
No instante t = 1 s, a aceleração da partícula será igual a -5 m/s 2 .
- C. Certo
- E. Errado
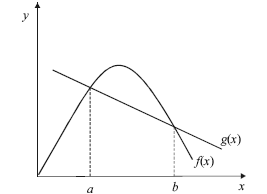
A figura acima ilustra os gráficos das funções f e g, em que f é uma função derivável e g é uma função linear. A partir desses gráficos, julgue os itens seguintes.
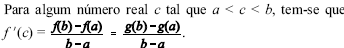
- C. Certo
- E. Errado
A função 
, derivada primeira da função f, é sempre decrescente.
- C. Certo
- E. Errado
Com base nessas informações, julgue os itens a seguir.
Em x = 0, a função f tem um ponto de mínimo local.
- C. Certo
- E. Errado
Com relação à equação diferencial y" + 4y' + 3y = 0, assinale a opção correta.
- A.
Todas as raízes da equação característica são números complexos não reais.
- B.
A equação diferencial admite solução que seja uma função trigonométrica.
- C.
As soluções elementares da equação diferencial são funções exponenciais reais.
- D.
A equação admite solução da forma polinomial, com coeficientes reais.
A solução do problema de valor inicial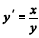 
, y(0) = 1 é uma função y = f (x) que satisfaz a relação
- A.
y2 = x2 .
- B.
y2 = 1 - x2 .
- C.
y2 = x2 - 1.
- D.
y2 = x2 + 1.
A aceleração da partícula em t = 2 s é igual a 3 m/s2.
- C. Certo
- E. Errado
O Provas e Concursos é um banco de dados de questões de concursos públicos organizadas por matéria, assunto, ano, banca organizadora, etc
