Questões sobre Geometria

Na metodologia de ensino e aprendizagem de áreas de figuras planas, deve-se considerar dois aspectos importantes:

I o cálculo da área utilizando determinada unidade de medida;

 II o cálculo da área por meio do processo de decomposição e recomposição da figura. No primeiro aspecto, o uso de malhas quadriculadas ou triangulares ajuda na construção do conceito de área e, no segundo, a decomposição da figura torna importante o trabalho com diferentes tipos de tangramas.

Com o objetivo de trabalhar esses aspectos, um professor preparou um conjunto de atividades utilizando uma malha, como a ilustrada na figura abaixo, formada por triângulos eqüiláteros.

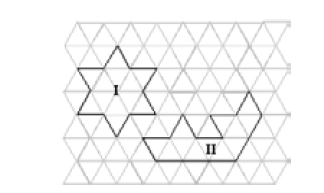
A partir das informações e da malha ilustrada acima, na qual foram desenhados os polígonos I e II, julgue os itens que se seguem.

Os polígonos I e II têm o mesmo perímetro.

• C. Certo
• E. Errado

Na metodologia de ensino e aprendizagem de áreas de figuras planas, deve-se considerar dois aspectos importantes:

I o cálculo da área utilizando determinada unidade de medida;

 II o cálculo da área por meio do processo de decomposição e recomposição da figura. No primeiro aspecto, o uso de malhas quadriculadas ou triangulares ajuda na construção do conceito de área e, no segundo, a decomposição da figura torna importante o trabalho com diferentes tipos de tangramas.

Com o objetivo de trabalhar esses aspectos, um professor preparou um conjunto de atividades utilizando uma malha, como a ilustrada na figura abaixo, formada por triângulos eqüiláteros.

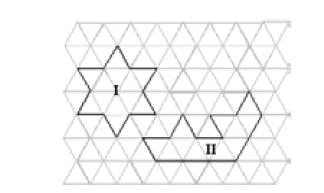
A partir das informações e da malha ilustrada acima, na qual foram desenhados os polígonos I e II, julgue os itens que se seguem.

A área do polígono II é inferior à área do polígono I.

• C. Certo
• E. Errado

Os tangramas são materiais pedagógicos que auxiliam no ensino e aprendizagem de números racionais, áreas e perímetros de figuras planas. O tangrama na forma de um coração, ilustrado na figura abaixo, é formado por uma quadrado de lado AB, um trapézio, um paralelogramo, um triângulo e dois semi-círculos de mesmo raio AB.

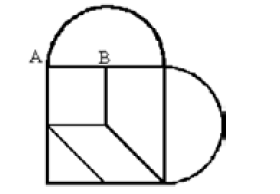
 Com base nessas informações, na figura acima e considerando que a medida do segmento AB é 1 cm, julgue os itens a seguir.

A área do trapézio é igual a 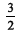  cm2.

• C. Certo
• E. Errado

É possível desenhar um losango em que os lados estejam sobre os segmentos de retas da malha e que a 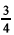 área seja igual a da área do polígono II.

• C. Certo
• E. Errado

Se o comprimento de cada lado do triângulo da malha fosse igual a 10 cm, então o perímetro do polígono I seria igual a 1,2 m.

• C. Certo
• E. Errado

Os polígonos I e II têm o mesmo perímetro.

• C. Certo
• E. Errado

Existe uma decomposição do polígono I, em dois polígonos congruentes, de 7 lados, e que podem ser utilizados para formar o polígono II.

• C. Certo
• E. Errado

Na situação apresentada, se C divide o segmento AB em média extrema razão, então o quociente entre a área do retângulo de lados iguais aos segmentos AB e CB e a área do quadrado de lados iguais a AC é igual

• A.

  

• B.

  k

• C.

  

• D.

  1.

Uma professora solicitou a seus alunos que utilizassem peças cúbicas, todas iguais, para construírem sólidos. Um aluno construiu um paralelepípedo retângulo utilizando 16 peças na base e a altura era igual a 4 vezes a altura dos cubos. Nessa situação, é correto afirmar que

o volume do sólido construído pelo aluno é igual a 32 vezes o volume de uma das peças.

• C. Certo
• E. Errado

Texto para as questões 42 e 43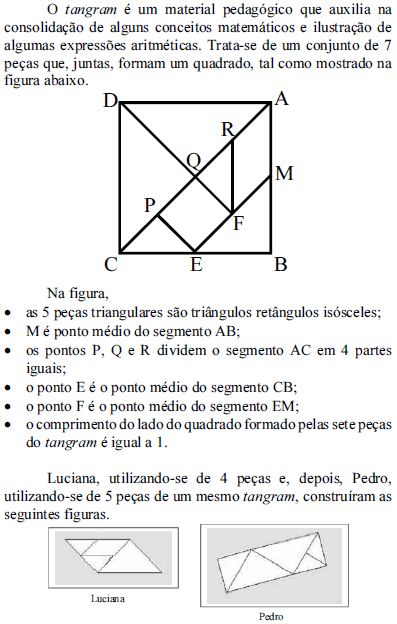

A partir das informações acima, é correto afirmar que o quociente entre a área do paralelogramo construído por Luciana e a área do retângulo construído por Pedro é igual a

• A.

  

• B.

  

• C.

  

• D.