Questões sobre Retas e Planos

Avalie as afirmativas a seguir, a respeito de pontos, retas e planos:

I - Existe uma única reta que passa por dois pontos distintos.
II - Existe um único plano que passa por três pontos distintos.
III - Dados três pontos não colineares, existe uma única reta que passa por um dos pontos e é paralela à reta que passa pelos outros dois.
IV - Se dois planos são paralelos, então qualquer reta que esteja num dos planos é paralela a todas as retas que estão no outro plano.

Estão corretas as afirmativas:

• A.

  I e II, apenas;

• B.

  II e IV, apenas;

• C.

  I, II e III, apenas;

• D.

  II, III e IV, apenas;

• E.

  I, III e IV, apenas.

Considere o paralelogramo ABCD representado na figura abaixo.

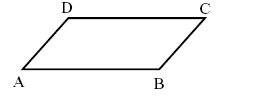
Considere as retas

 -  r que passa por A e B;

 -  s que passa por B e C;

 -  t que passa por A e D;

 -  u que passa por B e D; 

 -  v que passa por A e C.

Analise as afirmativas abaixo:

I – u é perpendicular à v;

II – t é paralelo à s;

III – r é perpendicular à s.

É/são verdadeira(s) somente:

• A. I;
• B. II;
• C. I e II;
• D. II e III;
• E. I, II e III.

NAS QUESTÕES NUMERADAS DE 06 A 10, ASSINALE A ÚNICA ALTERNATIVA CORRETA.

O campo de futebol abaixo é representado por qual forma geométrica plana e qual o perímetro desse campo?

• A. Retângulo e 420 m
• B. Quadrado e 420 m
• C. Retângulo e 320 m
• D. Quadrado e 320 m

NAS QUESTÕES NUMERADAS DE 06 A 10, ASSINALE A ÚNICA ALTERNATIVA CORRETA.

Calcule a área do campo de futebol desenhado abaixo e assinale a alternativa correta:

• A. 8.350 m²
• B. 7.250 m²
• C. 8.150 m²
• D. 8.250 m²

P é um plano e r é uma reta perpendicular a P. Quantos são os planos que contêm r e são perpendiculares a P?

• A. 0
• B. 1
• C. 2
• D. 3
• E. infinitos

As retas r e s são paralelas entre si. As retas t e u são perpendiculares à reta r. As interseções dessas 4 retas determinam o retângulo ABCD indicado na figura abaixo.

• A.

  2 ou 3 partes;

• B.

  3 ou 6 partes;

• C.

  exatamente 2 partes;

• D.

  exatamente 3 partes;

• E.

  exatamente 6 partes.

No espaço tridimensional, é sempre verdade que

• A.

  se dois planos forem perpendiculares, toda reta paralela a um deles será perpendicular ao outro.

• B.

  se dois planos são paralelos, toda reta perpendicular ao primeiro é perpendicular ao segundo.

• C.

  se uma reta é paralela a um plano, ela é paralela a todas as retas desse plano

• D.

  se duas retas são paralelas, toda reta que encontra a primeira encontra a segunda.

• E.

  se duas retas são paralelas a uma terceira, elas são perpendiculares entre si.

Os segmentos AB e CD são perpendiculares e se interceptam no ponto E comum aos dois segmentos. Se BE = CE e AE = DE e as áreas dos triângulos CBE e ADE são, respectivamente, 10m² e 8m² , a distância de B até D é igual a

• A.

  3m

• B.

  6m

• C.

  4m

• D.

  5m

• A.

  120°;

• B.

  135°;

• C.

  145°;

• D.

  150°;

• E.

  160°.

As retas r e s são paralelas entre si. As retas t e u são perpendiculares à reta r. As interseções dessas 4 retas determinam o retângulo ABCD indicado na figura abaixo.

Se adicionarmos 3 retas 1 l , 2 l e 3 l não coincidentes entre si nem coincidentes com as retas r, s, t, u e que, além disso, satisfaçam:

 – 1 l é paralela a u;

– 2 l é perpendicular a r;

 – 3 l é paralela a s;

 – o segmento BC é interceptado pelo menos uma vez;

 – o segmento AB não é interceptado.

Concluímos que o retângulo ABCD foi dividido por estas três retas em:

• A.

  2 ou 3 partes;

• B.

  3 ou 6 partes;

• C.

  exatamente 2 partes;

• D.

  exatamente 3 partes;

• E.

  exatamente 6 partes.