Questões sobre Trigonometria

Na Matemática, o conceito de função é freqüentemente utilizado para a modelagem de situações-problema reais. Com respeito a funções tradicionais e bem conhecidas, julgue os itens subseqüentes.

Sabendo que tg =  , então a altura do muro representado na figura abaixo é igual a 3 m.

• C. Certo
• E. Errado

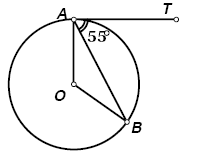
Na figura abaixo, AT é tangente à circunferência de centro O no ponto A. Sabendo-se que a tangente AT faz um ângulo de 55º com a corda AB, podemos afirmar que o ângulo AÔB, em graus, mede:

• A. 90º
• B. 95º
• C. 100º
• D. 105º
• E. 110º

No triângulo retângulo abaixo, o valor do sen a é

• A. 0,50
• B. 0,80
• C. 0,75
• D. 0,60
• E. 0,90

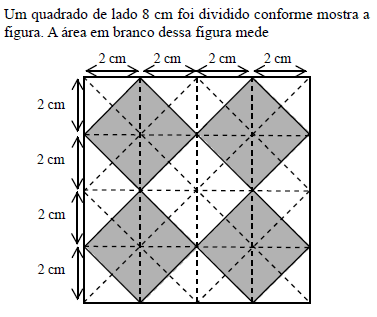
• A. 32 cm².
• B. 30 cm².
• C. 28 cm².
• D. 26 cm².
• E. 24 cm².

A) ?, pois sen (?) = 0.

B) ?/2, pois sen (?/2) = 0.

C) ?/2, pois cos (?/2) = 0.

D) ?/4, pois sen (?/4) = cos (?/4).

Os sábios gregos relacionaram os Números Naturais com as formas geométricas. Para exemplificar, a seguir é apresentada a seqüência de quantidades que formam triângulos eqüiláteros, sendo chamados de números triangulares: 1, 3, 6, 10, ... . Observando-se a seqüência, pode-se afirmar que a opção que apresenta o oitavo número triangular é:

• A.

  28

• B.

  36

• C.

  38

• D.

  42

• E.

  44

Um valor de x tal que (senx)(cosx)= é:

• A.

  10⁰

• B.

  15⁰

• C.

  20⁰

• D.

  25⁰

Sendo tg x = 3, qual o valor da expressão: cos2x + sen2x. sec²x + sen²x ?

• A.

  10

• B.

  9

• C.

  4

• D.

  3

• E.

  2

Um engenheiro deseja medir a largura de uma avenida num momento de grande movimento. Não podendo efetuar a medida diretamente, ele utiliza um teodolito e uma trena. Posicionando-se de um dos lados da avenida (ponto B) ele usa um poste como ponto de referência do outro lado (ponto A), desloca-se perpendicularmente à linha reta que liga o poste ao ponto B, por 5m (até o ponto C) e mede o ângulo entre sua nova posição e o poste referência, obtendo 55o, como demonstra o esquema abaixo:

O engenheiro consulta a seguinte tabela:

Qual a largura da avenida?

• A.

  2,86m

• B.

  4,10m

• C.

  5,15m

• D.

  7,14m

• E.

  8,16m

O valor de cos 240º é igual a:

• A.

  - 1 2

• B.

  1 2

• C.

  - v3 2

• D.

  v3 2