Questões sobre Trigonometria
Lista completa de Questões sobre Trigonometria para resolução totalmente grátis. Selecione os assuntos no filtro de questões e comece a resolver exercícios.
Um garoto, localizado no ponto A da figura, impulsiona um skate percorrendo 2,5 m até uma rampa de 1,5 m de altura, chegando até o topo da mesma, no ponto B, e retornando ao ponto de partida.
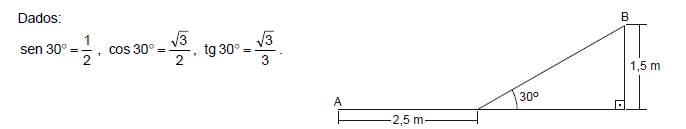
Nessas condições, podemos concluir que esse garoto percorreu, no total:
- A.
8 m
- B.
11 m
- C.
13 m
- D.
15 m
- E.
17 m
Seja x um arco do 1o quadrante, tal que sen x + cos 60° = 1. Afirma-se que tg x é igual a
- A.
- B.
- C.
1/2
- D.
1
- E.
No triângulo ABC representado na figura abaixo, os segmentos BT e CT dividem os respectivos ângulos nternos dos vértices B e C em partes iguais.
Se o ângulo do vértice A mede 80°, a medida θ do ângulo assinalado é igual a
- A.
110°.
- B.
120°.
- C.
130°.
- D.
140°.
- E.
150°.
Texto e figura para as questões 41 e 42
No experimento esquematizado, e assumindo c = 3 × 108 m/s (velocidade da luz), o deslocamento s percorrido pelo feixe luminoso satisfaz à condição
- A.
- B.
- C.
- D.
Texto e figura para as questões 41 e 42
- A.
α.
- B.
2α.
- C.
3α.
- D.
Matemática - Trigonometria - Fundação para o Vestibular da Universidade Estadual Paulista (VUNESP) - 2010
Um terreno retangular com área de 192 m2 tem um dos lados medindo 4 m a mais que o outro. Dentro desse terreno, foi colocada uma cerca a 1 m dos lados do terreno, demarcando assim uma área retangular menor, como mostra a figura sem escala. A área demarcada é, em m2, igual a
- A.
132.
- B.
140.
- C.
156.
- D.
160.
- E.
184.
Matemática - Trigonometria - Fundação para o Vestibular da Universidade Estadual Paulista (VUNESP) - 2010
A figura sem escala mostra a planta de um calçadão no centro de uma pequena cidade. Um pedestre, saindo de A, pode chegar até B de duas formas distintas, ou seja, contornando a praça triangular pela esquerda ou pela direita. Se o pedestre caminhar por qualquer dos trajetos indicados pelas linhas retas tracejadas, percorrerá a mesma distância em ambos os casos. Os comprimentos de dois trechos retos dos trajetos são dados na figura. Sabendo que a soma dos comprimentos x e y dos trechos delimitados pelas setas na planta é igual a 12 m, a razão 
pode ser expressa pela fração
- A.
- B.
- C.
- D.
- E.
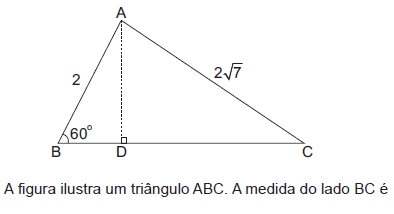
- A. 4
- B. 5
- C. 6
- D.
- E.
Deslocando-se C, em relação ao sistema cartesiano, verticalmente para cima 3 unidades, a equação da catenária passa a ser
- A. y = cosh(x)
- B. y = cosh(x) + 2
- C. y = cosh(x) + 3
- D. y = cosh(x - 3) - 1
- E. y = cosh(x + 3) - 1
O Provas e Concursos é um banco de dados de questões de concursos públicos organizadas por matéria, assunto, ano, banca organizadora, etc
