Questões de Matemática da Centro de Seleção e de Promoção de Eventos UnB (CESPE)

O mapa do estado do Mato Grosso do Sul (MS) está desenhado na figura I à baixo, na escala 1:10.000.000, ou seja, 1 cm na figura corresponde a 10.000.000 cm no tamanho real. Nesse mapa, estão representadas as rodovias federais que cortam esse estado. Na figura II, apresentada na mesma escala, para efeito de simplificação, os trechos das rodovias no interior do estado estão representados por segmentos de reta, admitindo-se que toda a região seja plana. No modelo representado na figura II, considere que os comprimentos dos segmentos AF, AD e CD sejam, respectivamente, iguais a 1,8 cm, 1,2 cm e 1,7 cm. Além disso, suponha que o trapézio ABCD seja isósceles, o triângulo ADE seja retângulo em D, o comprimento de EF esteja para o comprimento de AF assim como 1 está para 6 e que o ângulo ADC seja igual a 60º. De acordo com o modelo proposto e com o Código de Trânsito Brasileiro (CTB), julgue os itens abaixo.

Considere a seguinte situação.

Na figura II, traça-se um sistema de eixos perpendiculares com origem no ponto D, em que o eixo das abscissas x contém o segmento AD, o eixo das ordenadas y contém o segmento DE e uma unidade de medida em cada um desses eixos corresponde a 1 cm. Nesse sistema, o ponto A tem abscissa igual a 1,2, enquanto E tem ordenada negativa.

Nessa situação, a poligonal DCB é o gráfico da função

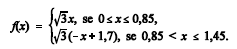
• C. Certo
• E. Errado

O mapa do estado do Mato Grosso do Sul (MS) está desenhado na figura I à baixo, na escala 1:10.000.000, ou seja, 1 cm na figura corresponde a 10.000.000 cm no tamanho real. Nesse mapa, estão representadas as rodovias federais que cortam esse estado. Na figura II, apresentada na mesma escala, para efeito de simplificação, os trechos das rodovias no interior do estado estão representados por segmentos de reta, admitindo-se que toda a região seja plana. No modelo representado na figura II, considere que os comprimentos dos segmentos AF, AD e CD sejam, respectivamente, iguais a 1,8 cm, 1,2 cm e 1,7 cm. Além disso, suponha que o trapézio ABCD seja isósceles, o triângulo ADE seja retângulo em D, o comprimento de EF esteja para o comprimento de AF assim como 1 está para 6 e que o ângulo ADC seja igual a 60º. De acordo com o modelo proposto e com o Código de Trânsito Brasileiro (CTB), julgue os itens abaixo.

O tamanho real do trajeto correspondente a DEF é superior a 85 km.

• C. Certo
• E. Errado

Considere as seguintes acepções da palavra função, reproduzidas de três dicionários da língua portuguesa.

Com base nas acepções acima, no conceito matemático de função e no CTB, julgue os itens que se seguem.

De acordo com o conceito matemático, a correspondência entre as infrações de trânsito cometidas e os valores das multas a elas atribuídas é uma função injetora.

• C. Certo
• E. Errado

Texto IV- questões 9 e 10

Com base nas informações apresentadas no texto IV, julgue os itens abaixo.

Se p(v) representa a probabilidade de morte da vítima de um atropelamento no qual a velocidade de colisão, em km/h, é igual a v, então os números p(40), p(50), p(60), p(70) e p(80) estão, nessa ordem, em progressão geométrica.

• C. Certo
• E. Errado

Com base no regime de juros simples, julgue os itens seguintes.

O valor nominal de uma duplicata, cujo desconto racional feito à taxa de 60% ao ano, 2 meses antes do vencimento, resultou em um valor descontado de R$ 70.000,00, é inferior a R$ 80.000,00.

• C. Certo
• E. Errado

Texto IV- questões 9 e 10

Com base nas informações apresentadas no texto IV, julgue os itens abaixo.

É impossível encontrar números reais a, b e c tais que o gráfico da função f(x) = ax² + bx + c coincida com o gráfico ilustrado na figura, em que x é a velocidade de colisão e f(x) é a probabilidade de morte.

• C. Certo
• E. Errado

Considerando que a produção de feijão (Y), em kg/ha, tenha relação com a quantidade de um determinado esterco (X), em t/ha, expressa pela equação Y = 30 + 40X • 2X² , e que os preços do feijão e do esterco sejam, respectivamente, iguais a R$ 2,00 o quilograma e a R$ 24,00 a tonelada, julgue os itens que se seguem.

Se o preço do esterco aumentar para R$ 36,00 a tonelada, a quantidade ótima do mesmo será de 1 t/ha.

• C. Certo
• E. Errado

Considerando que a produção de feijão (Y), em kg/ha, tenha relação com a quantidade de um determinado esterco (X), em t/ha, expressa pela equação Y = 30 + 40X • 2X² , e que os preços do feijão e do esterco sejam, respectivamente, iguais a R$ 2,00 o quilograma e a R$ 24,00 a tonelada, julgue os itens que se seguem.

A receita marginal que é obtida no ponto de máximo lucro é igual ao custo do esterco.

• C. Certo
• E. Errado

Considerando que a produção de feijão (Y), em kg/ha, tenha relação com a quantidade de um determinado esterco (X), em t/ha, expressa pela equação Y = 30 + 40X • 2X² , e que os preços do feijão e do esterco sejam, respectivamente, iguais a R$ 2,00 o quilograma e a R$ 24,00 a tonelada, julgue os itens que se seguem.

A produtividade marginal do esterco é de 12 kg/ha de feijão, quando se usam 7 t/ha do esterco.

• C. Certo
• E. Errado

Considerando que a produção de feijão (Y), em kg/ha, tenha relação com a quantidade de um determinado esterco (X), em t/ha, expressa pela equação Y = 30 + 40X • 2X² , e que os preços do feijão e do esterco sejam, respectivamente, iguais a R$ 2,00 o quilograma e a R$ 24,00 a tonelada, julgue os itens que se seguem.

O máximo lucro é atingido quando são colocadas 6 t/ha do esterco.

• C. Certo
• E. Errado