Questões sobre Análise Combinatória

Alberto, Bruno, Sérgio, Janete e Regina assistirão a uma peça de teatro sentados em uma mesma fila, lado a lado. Nessa situação, julgue os itens subsequentes.

A quantidade de maneiras distintas de como essas 5 pessoas poderão ocupar os assentos é igual a 120.

• C. Certo
• E. Errado

Alberto, Bruno, Sérgio, Janete e Regina assistirão a uma peça de teatro sentados em uma mesma fila, lado a lado. Nessa situação, julgue os itens subsequentes.

Caso Janete e Regina sentem-se nas extremidades da fila, então a quantidade de maneiras distintas de como essas 5 pessoas poderão ocupar os assentos é igual a 24.

• C. Certo
• E. Errado

Considerando 20 pontos sobre uma circunferência, em posições distintas, julgue os itens subsequentes.

Tendo vértices nesses 20 pontos, é possível formar 1.140 triângulos.

• C. Certo
• E. Errado

Considerando 20 pontos sobre uma circunferência, em posições distintas, julgue os itens subsequentes.

O polígono que tem vértices nesses 20 pontos tem 170 diagonais.

• C. Certo
• E. Errado

Considerando que devam ser escolhidas 3 aeronaves para inspeção e manutenção, sendo que não podem ser selecionadas as 2 aeronaves de uma mesma estação, e que todas as seis estações já possuam as duas aeronaves previstas, então o número de formas distintas de se fazer essa escolha será superior a 150.

• C. Certo
• E. Errado

Com base no texto acima, julgue os itens a seguir.

Se as vítimas indicadas na pesquisa totalizaram 250 pessoas, então o número de maneiras distintas de se escolher um grupo de 3 homens entre as vítimas será superior a 4.000.

• C. Certo
• E. Errado

De acordo com o primeiro lema de Kaplansky, a quantidade de subconjuntos de {1, 2, 3,..., n} com p elementos, em que não há números consecutivos, é dada pela fórmula abaixo.

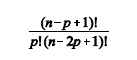
Uma das aplicações desse lema é a contagem do número de maneiras de se sentar 4 meninas e 6 meninos em uma fila de 10 cadeiras, de modo que 2 meninas não fiquem em posições adjacentes. A estratégia para se realizar essa contagem compreende quatro passos. Em primeiro lugar, deve-se contar o número de maneiras de se escolher 4 cadeiras sem que haja cadeiras consecutivas; esse procedimento deve ser feito utilizando-se o lema de Kaplansky. Em seguida, deve-se contar o número de maneiras de organizar as meninas nessas cadeiras. O próximo passo consiste em contar o número de maneiras de se distribuir os meninos nas cadeiras restantes. Por fim, deve-se usar o princípio multiplicativo.

Com base nessas informações, julgue os itens subsecutivos.

A partir dos dados acima, é correto concluir que o número de maneiras de se organizar as 4 meninas nas 4 cadeiras escolhidas é igual a 16.

• C. Certo
• E. Errado

De acordo com o primeiro lema de Kaplansky, a quantidade de subconjuntos de {1, 2, 3,..., n} com p elementos, em que não há números consecutivos, é dada pela fórmula abaixo.

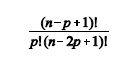
Uma das aplicações desse lema é a contagem do número de maneiras de se sentar 4 meninas e 6 meninos em uma fila de 10 cadeiras, de modo que 2 meninas não fiquem em posições adjacentes. A estratégia para se realizar essa contagem compreende quatro passos. Em primeiro lugar, deve-se contar o número de maneiras de se escolher 4 cadeiras sem que haja cadeiras consecutivas; esse procedimento deve ser feito utilizando-se o lema de Kaplansky. Em seguida, deve-se contar o número de maneiras de organizar as meninas nessas cadeiras. O próximo passo consiste em contar o número de maneiras de se distribuir os meninos nas cadeiras restantes. Por fim, deve-se usar o princípio multiplicativo.

Com base nessas informações, julgue os itens subsecutivos.

Em face dos dados apresentados, é correto afirmar que o número de maneiras de se escolher as 4 cadeiras entre as 10 disponíveis sem que haja cadeiras consecutivas é superior a 40.

• C. Certo
• E. Errado

De acordo com o primeiro lema de Kaplansky, a quantidade de subconjuntos de {1, 2, 3,..., n} com p elementos, em que não há números consecutivos, é dada pela fórmula abaixo.

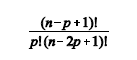
Uma das aplicações desse lema é a contagem do número de maneiras de se sentar 4 meninas e 6 meninos em uma fila de 10 cadeiras, de modo que 2 meninas não fiquem em posições adjacentes. A estratégia para se realizar essa contagem compreende quatro passos. Em primeiro lugar, deve-se contar o número de maneiras de se escolher 4 cadeiras sem que haja cadeiras consecutivas; esse procedimento deve ser feito utilizando-se o lema de Kaplansky. Em seguida, deve-se contar o número de maneiras de organizar as meninas nessas cadeiras. O próximo passo consiste em contar o número de maneiras de se distribuir os meninos nas cadeiras restantes. Por fim, deve-se usar o princípio multiplicativo.

Com base nessas informações, julgue os itens subsecutivos.

Diante dos dados acima, é correto afirmar que o número de maneiras de se sentar 4 meninas e 6 meninos em uma fila de 10 cadeiras, de modo que não fiquem 2 meninas em posições adjacentes, é superior a 600.000.

• C. Certo
• E. Errado

A quantidade de caracteres braille distintos que podem ser formados pelo aumento do relevo de apenas dois pontos em uma tecla é igual a 30.

• C. Certo
• E. Errado