Questões de Raciocínio lógico da Fundação Carlos Chagas (FCC)

Uma pilha com 14 cartas tem em cada uma delas um número natural impresso em uma de suas faces e que vão do 1 ao 14. O número está voltado para cima e as cartas estão dispostas em ordem decrescente. A carta com o número 14 está em cima da pilha, visível, embaixo dela está a carta 13, assim por diante até chegar a carta 1, a que está embaixo de todas. Sua interferência na pilha de cartas é que você passa as duas cartas que estão em cima da pilha para baixo da pilha, uma de cada vez e exclui da pilha a carta seguinte. Repete esse procedimento de passar duas cartas para baixo da pilha, uma de cada vez, e excluir da pilha a carta seguinte até excluir a carta com o número 14. Após a exclusão da carta com o número 14, o número de cartas que ainda estão na pilha é

• A.

  7.

• B.

  3.

• C.

  9.

• D.

  8.

• E.

  10.

Considere um sistema de referência com apenas duas posições que serão chamadas de vertical (V) e horizontal (H). Imagine um trem de brinquedo composto por apenas quatro vagões. Esses vagões estão ordenados e ocupam apenas as posições V e H. Uma primeira informação sobre as posições dos vagões mostra o primeiro vagão na posição V, o segundo na posição H, o terceiro na posição V e o quarto na posição V, formando a sequência: V, H, V, V para os vagões. Serão fornecidas outras cinco novas informações sobre as posições dos vagões em forma de sequência das letras V e H.

2^a informação: V, V, H, V;

3^a informação: H, V, V, H;

4^a informação: V, H, V, V;

5^a informação: V, V, H, V; 6a informação: H, V, V, H;

Supondo que as informações sobre as posições continuem seguindo o mesmo padrão, a sequência que identifica a 10^a informação é

• A.

  V, H, H, V.

• B.

  V, V, H, V.

• C.

  H, V, V, H.

• D.

  V, H, V, V.

• E.

  H, V, H, V.

Um jogo entre duas pessoas consiste em que cada um dos participantes risque palitos desenhados em uma folha de papel. Cada jogador, em sua jogada, tem que riscar pelo menos um palito, e pode riscar até cinco palitos. O jogador que riscar o último palito perde o jogo. Alguns exemplos do jogo: se o jogo começar com dois palitos a serem riscados e o 1º jogador riscar um palito, o 2º jogador risca o último palito e perde. O jogo pode começar com três palitos. Se, nesse caso, o 1o jogador risca dois palitos na sua jogada, e o 2º jogador risca o último palito e perde, ou se o 1º jogador risca apenas um palito, o 2º jogador risca um palito e deixa o último palito para o 1º jogador riscar e perder. Se o jogo iniciar com oito palitos, e para não dar qualquer chance de vitória ao 2º jogador, o número de palitos que o 1º jogador deverá riscar é

• A.

  3.

• B.

  5.

• C.

  4.

• D.

  1.

• E.

  2.

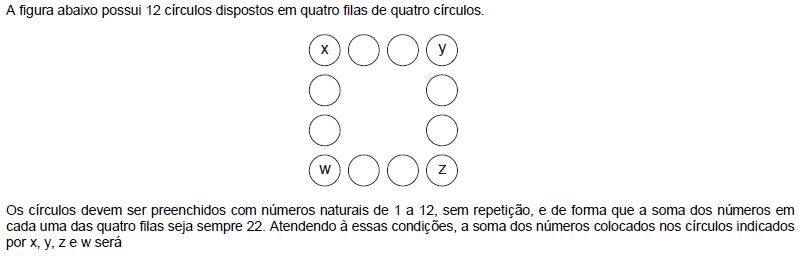
• A.

  8.

• B.

  12.

• C.

  4.

• D.

  10.

• E.

  6.

• A.

  1.

• B.

  2.

• C.

  3.

• D.

  9.

• E.

  18.

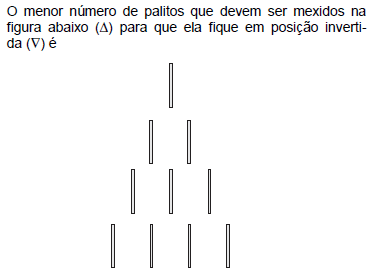
• A.

  1.

• B.

  3.

• C.

  2.

• D.

  5.

• E.

  4.

Seis pessoas, dentre as quais está Elias, estão aguardando em uma fila para serem atendidas pelo caixa de uma loja. Nesta fila, Carlos está à frente de Daniel, que se encontra imediatamente atrás de Bruno. Felipe não é o primeiro da fila, mas está mais próximo do primeiro lugar do que do último. Sabendo que Ari será atendido antes do que Carlos e que Carlos não é o quarto da fila, pode-se concluir que a pessoa que ocupa a quarta posição da fila

• A.

  certamente é Bruno.

• B.

  certamente é Daniel.

• C.

  certamente é Elias.

• D.

  pode ser Bruno ou Daniel.

• E.

  pode ser Bruno ou Elias.

Para realizar uma tarefa em grupos, era necessário separar os participantes em dois tipos de grupos. A diferença entre o número de participantes de dois grupos diferentes é um elemento. A quantidade de grupos com maior número de elementos deve ser um a menos do que a quantidade do outro tipo de grupo. O coordenador dos grupos verificou, a partir do total de participantes do projeto, que poderia realizar a divisão em grupos e seriam 8 grupos com número menor de participantes. Levando em conta que o total de participantes era a primeira possibilidade menor que 156, o número total de participantes dos grupos maiores é de

• A.

  72.

• B.

  66.

• C.

  68.

• D.

  70.

• E.

  56.

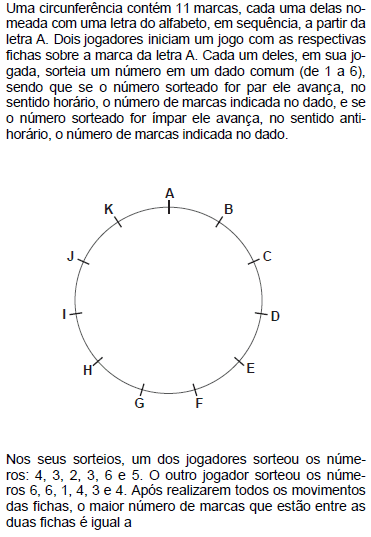
• A.

  9.

• B.

  6.

• C.

  8.

• D.

  7.

• E.

  5.

Ao se admitir por verdadeira a declaração “Se Paulo é alto, então Gabriela não é alta”, conclui-se, de maneira correta e necessária, que se

• A.

  Gabriela é alta, então Paulo não é alto.

• B.

  Gabriela é alta, então Paulo é alto.

• C.

  Gabriela não é alta, então Paulo não é alto.

• D.

  Gabriela não é alta, então Paulo é Gabriela.

• E.

  Paulo não é alto, então Gabriela é maior que Paulo.