Questões de Raciocínio lógico da Fundação Carlos Chagas (FCC)

Para recepcionar os 37 novos funcionários de uma agência, foi criada uma brincadeira na qual os novos funcionários deveriam ser divididos em grupos iguais (mesmo número de integrantes) que poderiam ter ou 5, ou 7, ou 8, ou 9, ou 10 integrantes. Das cinco opções de tamanhos dos grupos, a que deixa menos funcionários sem grupo é aquela em que os grupos têm número de integrantes igual a

• A. 7.
• B. 9.
• C. 5.
• D. 10.
• E. 8.

• A.

  34/495.

• B.

  34/990.

• C.

  37/990.

• D.

  478/512.

• E.

  34/512.

Após a finalização de um concurso de conhecimentos gerais, os dados foram organizados e apresentados em um infográfico, conforme abaixo.

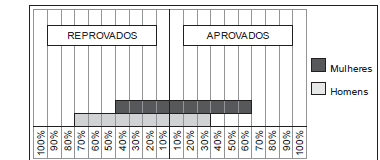
Sabe-se que, do total de 840 participantes desse exame, 25% eram mulheres. Nas condições dadas, o total de aprovados no concurso é igual a

• A. 756.
• B. 315.
• C. 189.
• D. 284.
• E. 354.

• A.

  I e II, apenas.

• B.

  I, apenas.

• C.

  III, apenas.

• D.

  II, apenas.

• E.

  I, II e III.

Em uma loja de bijuterias, todos os produtos são vendidos por um dentre os seguintes preços: R$ 5,00, R$ 7,00 ou R$ 10,00. Márcia gastou R$ 65,00 nessa loja, tendo adquirido pelo menos um produto de cada preço. Considerando apenas essas informações, o número mínimo e o número máximo de produtos que Márcia pode ter comprado são, respectivamente, iguais a

• A.

  9 e 10.

• B.

  8 e 11.

• C.

  8 e 10.

• D.

  9 e 13.

• E.

  7 e 13.

A rede de supermercados “Mais Barato” possui lojas em 10 estados brasileiros, havendo 20 lojas em cada um desses estados. Em cada loja, há 5.000 clientes cadastrados, sendo que um mesmo cliente não pode ser cadastrado em duas lojas diferentes. Os clientes cadastrados recebem um cartão com seu nome, o nome da loja onde se cadastraram e o número “Cliente Mais Barato”, que é uma sequência de quatro algarismos. Apenas com essas informações, é correto concluir que, necessariamente,

• A.

  existe pelo menos um número “Cliente Mais Barato” que está associado a 100 ou mais clientes cadastrados.

• B.

  os números “Cliente Mais Barato” dos clientes cadastrados em uma mesma loja variam de 0001 a 5000.

• C.

  não há dois clientes cadastrados em um mesmo estado que possuam o mesmo número “Cliente Mais Barato”.

• D.

  existem 200 clientes cadastrados no Brasil que possuem 0001 como número “Cliente Mais Barato”.

• E.

  não existe um número “Cliente Mais Barato” que esteja associado a apenas um cliente cadastrado nessa rede de supermercados.

Sobre uma circunferência desenhada no chão foram colocadas três placas. Uma com a letra A, outra com a B e outra com a C. As placas foram colocadas em posições equidistantes e ordenadas alfabeticamente no sentido horário. Também em posições equidistantes, ordenadas em ordem crescente e no sentido horário foram colocadas sobre a circunferência as placas com os números 1, outra com o número 2 e outra com o número 3, sendo que a placa com o número 1 foi colocada entre as placas A e B. Seis novas placas: D, E, F, G, H, I, foram colocadas sobre a circunferência com os mesmos condicionantes que as placas A, B e C. A placa D foi colocada entre as placas A e a placa 1, a placa E foi colocada entre as placas 1 e B e assim por diante. Doze novas placas: 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, foram colocadas sobre a circunferência com os mesmos condicionantes que as placas 1, 2 e 3. A placa 4 foi colocada entre as placas A e D, a placa 5 foi colocada entre a placa D e 1 e assim por diante. Ao final foram retiradas todas as placas cujos números são múltiplos de 3. Dessa maneira os pares de placas com letras que NÃO possuem placas com números entre elas na circunferência são:

• A.

  AI e CH.

• B.

  DE e AI.

• C.

  CH e BF.

• D.

  BE e GC.

• E.

  AD e HI.

Em um campeonato de futebol, as equipes ganham 5 pontos sempre que vencem um jogo, 2 pontos em caso de empate e 0 ponto nas derrotas. Faltando apenas ser realizada a última rodada do campeonato, as equipes Bota, Fogo e Mengo totalizam, respectivamente, 68, 67 e 66 pontos, enquanto que a quarta colocada possui menos de 60 pontos. Na última rodada, ocorrerão os jogos:

Fogo x Fla e Bota x Mengo

Sobre a situação descrita, considere as afirmações abaixo, feitas por três torcedores

I. Se houver uma equipe vencedora na partida Bota x Mengo, ela será, necessariamente, a campeã.

II. Para que a equipe Fogo seja a campeã, basta que ela vença a sua partida.

III. A equipe Bota é a única que, mesmo empatando, ainda poderá ser a campeã.

Está correto o que se afirma em

• A.

  I e II, apenas.

• B.

  I, apenas.

• C.

  III, apenas.

• D.

  II, apenas.

• E.

  I, II e III.

• A.

  1 e 4.

• B.

  5 e 8.

• C.

  9 e 12.

• D.

  13 e 16.

• E.

  17 e 20.

Uma senha formada por três letras distintas de nosso alfabeto possui exatamente duas letras em comum com cada uma das seguintes palavras: ARI, RIO e RUA. Em nenhum dos três casos, porém, uma das letras em comum ocupa a mesma posição na palavra e na senha. A primeira letra dessa senha é

• A.

  R

• B.

  O

• C.

  L

• D.

  I

• E.

  A