Questões de Estatística

A média geométrica dos números 4, 8 e 16 é

• A.

  maior que a respectiva média aritmética.

• B.

  inferior a 6.

• C.

  igual a 8.

• D.

  igual a 4.

• E.

  superior a 9.

Em relação à Amostragem Aleatória Simples, é INCORRETO afirmar que

• A. se os elementos da amostra são tomados sem reposição, a variância da média amostral depende do tamanho da população.
• B. se os elementos da amostra são tomados com reposição, a variância da média amostral não depende do tamanho da população.
• C. a média amostral é um estimador não viciado da média populacional em ambos os procedimentos, com ou sem reposição dos elementos tomados da população.
• D. para tamanho de amostra igual a 1 (um), a variância da média amostral é a mesma nos procedimentos com e sem reposição dos elementos tomados da população.
• E. para tamanho de amostra maior que um, a variância da média amostral é menor quando os elementos da amostra são tomados com reposição do que quando os elementos da amostra são tomados sem reposição.

• A. 2 ou − 2.
• B. 1,5 ou −1,5.
• C. 1 ou −1.
• D. 2 ou 1.
• E. 2 ou 1,5.

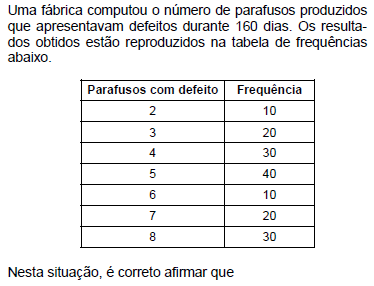
• A.

  a média aritmética dessa distribuição é menor que a mediana.

• B.

  multiplicando o número de parafusos com defeito por dois (2), o desvio padrão da nova distribuição também será multiplicado por dois (2) em relação à distribuição original.

• C.

  a moda dessa distribuição é superior à mediana.

• D.

  dividindo-se pela metade o número de parafusos com defeito, a variância da nova distribuição será dividida pela metade em relação à distribuição original.

• E.

  somando-se dois (2) às frequências da tabela, o desvio padrão e a variância da nova distribuição serão duas unidades maiores em relação aos da distribuição original.

A tabela a seguir apresenta algumas estatísticas descritivas do “peso” e do “comprimento” de 20 sapos.

É correto afirmar que os sapos têm

• A. menor variabilidade no “peso” do que no “comprimento”, pois a variância do “peso” é menor que a variância do “comprimento”.
• B. menor variabilidade no “peso” do que no “comprimento”, pois a variância do “peso” é menor que a variância do “comprimento”.
• C. menor variabilidade no “peso” do que no “comprimento”, pois a amplitude total do “peso” é menor que a amplitude total do “comprimento”.
• D. menor variabilidade no “peso” do que no “comprimento”, pois a amplitude total do “peso” é menor que a amplitude total do “comprimento”.
• E. maior variabilidade no “peso” do que no “comprimento”, pois a diferença absoluta entre a média e a mediana é menor no “peso” e menor que no “comprimento”.

U ma empresa produz componentes de dois tipos: A e B. Sejam as variáveis aleatórias: X = tempo de vida do componente A, em horas e Y = tempo de vida do componente B, em horas. De um lote de 120 componentes do tipo A e 80 componentes do tipo B, retira-se ao acaso um componente. Sabendo-se que X tem distribuição exponencial com média de 1.000 horas e que Y tem distribuição exponencial com média de 700 horas, a probabilidade do componente selecionado ter duração inferior a 1.400 horas é

• A. 0,569.
• B. 0,742.
• C. 0,618.
• D. 0,794.
• E. 0,634.

É correto afirmar que, no teste de hipóteses para comparar duas médias populacionais,

• A. os erros tipo I e tipo II são eventos complementares.
• B. quanto maior o nível de significância, maior será o valor – p.
• C. o poder do teste aumenta com a redução do tamanho da amostra.
• D. quanto menor o tamanho da amostra, menor será o nível de significância.
• E. o poder do teste aumenta com o aumento da diferença entre as médias populacionais.

• A. 0,2500.
• B. 0,1600.
• C. 0,0625.
• D. 0,0160.
• E. 0,0250.

Considere o teste T para testar a hipótese nula de que μ, a média de uma variável aleatória com distribuição Normal, seja igual a 0 (zero), usando o nível de significância igual a 0,05. É INCORRETO afirmar que

• A. o poder do teste é maior que 0,05 se μ for igual a 2 (dois).
• B. o cálculo do valor – p depende da definição da hipótese alternativa.
• C. a hipótese nula deve ser rejeitada se o valor – p for menor que 0,05.
• D. a estatística de teste tem distribuição T-de-Student com n graus de liberdade.
• E.

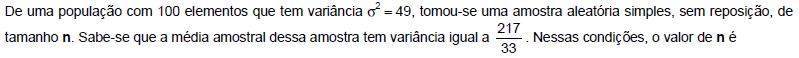
• A. 16.
• B. 49.
• C. 25.
• D. 7.
• E. 10.