Questões de Estatística

Um estudo acerca do sucateamento de veículos automotores forneceu o modelo abaixo para a probabilidade condicional de certo tipo de veículo estar em condição de uso em função do seu tempo de uso X (em anos).

P(Y = 1|X = t) = exp(-0,4 )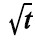

Nesse modelo, exp(.) representa a função exponencial; Y é uma variável aleatória binária que assume valor 1, se o veículo estiver em condição de uso, ou 0, se o veículo não estiver em condição de uso; t 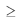 0 representa um instante (em anos) em particular; e a variável aleatória contínua X, é definida pela seguinte expressão.

P(X 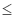 t) = 1 - exp(-0,5  )

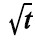 Com base nessas informações, julgue os itens que se seguem.

A média de X é superior a 7,5 e inferior a 8,5.

• C. Certo
• E. Errado

A mediana de W é maior que .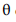

• C. Certo
• E. Errado

Considerando que Ana e Carlos candidataram-se a empregos em uma empresa e sabendo que a probabilidade de Ana ser contratada é igual a e que a probabilidade de ambos serem contratados é , julgue os itens subsequentes.

Se um dos dois for contratado, a probabilidade de que seja Carlos será igual a .

• C. Certo
• E. Errado

• A.
• B.

  

• C.

  

• D.

  

• E.

  

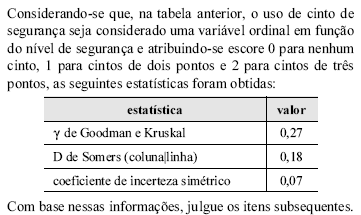
Em tabelas com dimensão 3 × 3, a estatística 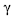 de Goodman e Kruskal é equivalente à estatística Q de Yule.

• C. Certo
• E. Errado

Um estudo acerca do sucateamento de veículos automotores forneceu o modelo abaixo para a probabilidade condicional de certo tipo de veículo estar em condição de uso em função do seu tempo de uso X (em anos).

P(Y = 1|X = t) = exp(-0,4 )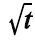

Nesse modelo, exp(.) representa a função exponencial; Y é uma variável aleatória binária que assume valor 1, se o veículo estiver em condição de uso, ou 0, se o veículo não estiver em condição de uso; t 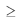 0 representa um instante (em anos) em particular; e a variável aleatória contínua X, é definida pela seguinte expressão.

P(X 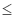 t) = 1 - exp(-0,5  )

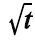 Com base nessas informações, julgue os itens que se seguem.

A média da variável aleatória W, em que W = exp(-0,4 ), é maior que 0,5.

• C. Certo
• E. Errado

Por meio de convênios com um plano de saúde e com escolas de nível fundamental e médio, uma empresa oferece a seus 3.000 empregados a possibilidade de adesão. Sabe-se que 300 empregados aderiram aos dois convênios, 1.700 aderiram ao convênio com as escolas e 500 não aderiram a nenhum desses convênios.

Em relação a essa situação, julgue os itens seguintes de 38 a 40.

Escolhendo-se ao acaso um dos empregados dessa empresa, a probabilidade de ele ter aderido a algum dos convênios é igual a  .

• C. Certo
• E. Errado

Em determinado mercado, duas corretoras, X e Y, são responsáveis por 40% e 60% do volume total de contratos negociados, respectivamente. Do volume correspondente das corretoras X e Y, 10% e 20%, respectivamente, são contratos futuros em dólar. Um contrato é selecionado ao acaso e verifica-se que é futuro em dólar. A probabilidade do mesmo ter sido negociado pela corretora Y é igual a:

• A.

  15%

• B.

  65%

• C.

  75%

• D.

  80%

Considere a variável aleatória bidimensional (X, Y) com função densidade conjunta dada por:

onde e é a base dos logaritmos naturais.

A esperança condicional de X dado y, denotada por E(X/y) é dada por

• A.

  

• B.

  e

• C.

  

• D.

  

• E.

  

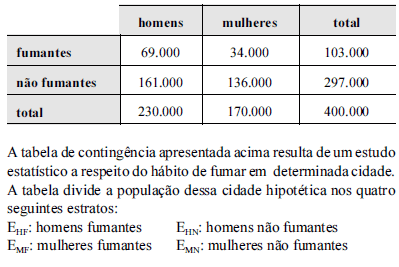
A partir dessas informações e da tabela apresentada, assinale a opção correta.

• A.

  Se o erro amostral tolerável é de 5%, uma amostra aleatória simples deve conter 300 pessoas.

• B.

  

• C.

  Para um erro amostral tolerável de 4%, o tamanho mínimo da amostra é menor que 625, qualquer que seja o tamanho da população.

• D.

  Se o tamanho de uma amostra estratificada proporcional é de 800, então a amostra consiste de 322 homens fumantes, 138 homens não fumantes, 68 mulheres fumantes e 272 mulheres não fumantes.

• E.

  Considerando-se os estratos acima, é correto afirmar que uma amostra estratificada proporcional contém 28% de fumantes.