Questões de Estatística

Com base na situação hipotética e no gráfico apresentados ao lado, julgue os itens a seguir.

Suponha que, para cada ano no período considerado, os dados apresentados são estimativas fornecidas por levantamentos amostrais de casas penais, seccionais e delegacias do estado. Cada elemento dessa amostra é classificado como superlotado ou não-superlotado. Para o primeiro caso, define-se que S = 1; para o segundo, S = 0. Nessa situação, S é uma variável binária e a média de S é uma estimativa da proporção de casas penais, seccionais e delegacias superlotadas do estado, no período considerado.

• C. Certo
• E. Errado

A correlação entre x e y é maior que 1.

• C. Certo
• E. Errado

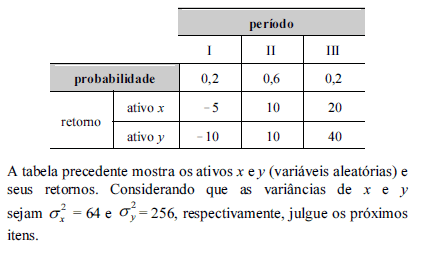O retorno esperado do ativo x é superior ao retorno esperado do ativo y.

• C. Certo
• E. Errado

A respeito de risco e retorno e dos resultados clássicos relacionados à teoria de carteiras, julgue os seguintes itens. O desvio padrão esperado de um portfólio é calculado a partir da média aritmética ponderada do desvio padrão de cada ativo que compõe o portfólio.

• C. Certo
• E. Errado

A respeito de risco e retorno e dos resultados clássicos relacionados à teoria de carteiras, julgue os seguintes itens. O risco de um portfólio composto por dois ativos reduz-se à medida que o coeficiente de correlação entre esses ativos aumenta.

• C. Certo
• E. Errado

Seja X uma variável aleatória com valor esperado μ e desvio padrão σ >0. Pode-se afirmar que

• A.

  pelo menos 75% das realizações de X pertencerão ao intervalo [μ-2σ; μ+2σ].

• B.

  pelo menos 80% das realizações de X pertencerão ao intervalo [μ-2σ; μ+2σ].

• C.

  pelo menos 90% das realizações de X pertencerão ao intervalo [μ-2σ; μ+2σ].

• D.

  pelo menos 95% das realizações de X pertencerão ao intervalo [μ-2σ; μ+2σ].

• E.

  apenas com o conhecimento de μ e σ não é possível fazer afirmação sobre o percentual de realizações de X que cairão no intervalo [μ-2σ; μ+2σ].

A respeito de risco e retorno e dos resultados clássicos relacionados à teoria de carteiras, julgue os seguintes itens. O retorno esperado médio de um portfólio é calculado a partir da média aritmética ponderada dos ativos que o compõem.

• C. Certo
• E. Errado

Seja X o peso em gramas da produção de uma variedade de soja. Sabe-se que o logaritmo neperiano de X – ln(X) tem distribuição normal com média 0,5 e variância 1. Seja F(x) a função de distribuição da normal padrão e b a constante tal que F(b)=60%. Assinale a opção que corresponde ao sexto decil de X, i.e, ao valor da constante q tal que P(X < q) = 60%.

• A.

  exp (0,5)

• B.

  exp (0,6)

• C.

  exp (b+0,5)

• D.

  b

• E.

  exp (b)

Com base na tabela precedente, que apresenta estatísticas referentes a duas variáveis observadas em um estudo previdenciário, julgue os seguintes itens.

O valor absoluto da covariância entre X e Y é igual ou inferior a 12.

• C. Certo
• E. Errado

A função geratriz de momentos da variável aleatória X vem dada para t suficientemente pequeno por

Assinale a opção correta.

• A.

  X tem valor esperado 2 e variância 1.

• B.

  X tem valor esperado 4 e variância 4.

• C.

  X tem distribuição exponencial.

• D.

  X tem distribuição beta.

• E.

  X tem distribuição uniforme em [2;4].