Questões de Estatística do ano 0000

A Cia. X presta serviço de manutenção preventiva nos computadores que vende. Em 18 chamadas para realização de serviços de manutenção foram observados os pares (x_i , y_i) onde x_i representa o número de máquinas examinadas na chamada e y_i o tempo gasto, em horas, na visita de inspeção. A tais observações ajusta-se o modelo linear x_i, com o uso de mínimos quadrados ordinários, sob a hipótese de erros com média zero, homoscedásticos, não correlacionados e com os x_i fixos (determinísticos). Foram obtidas as seguintes estatísticas para o ajuste: . As constantes a e b são as estimativas de mínimos quadrados de, respectivamente. Assinale a opção correspondente à estimativa não-viezada da variância residual.

• A. 3,6
• B. 4,7
• C. 1,0
• D. 0,7
• E. 1,2

Um técnico de uma empresa está interessado em desenvolver um modelo de regressão linear simples com o objetivo de prever o volume de vendas Y, medido em R$ 10.000,00, em função dos gastos com propaganda X, medidos em R$ 10.000,00. Neste contexto ajusta o modelo estatístico

aos dados da tabela abaixo. Os valores da tabela resultam de uma amostra de 10 meses escolhidos ao acaso.

A equação ajustada é dada por

46,5 + 52,6 X

(4,7)   (5,1)

onde os valores entre parênteses representam as estatísticas t dos testes das hipóteses de que os parâmetros correspondentes sejam nulos. A variância residual é estimada por 46,7 e a soma dos quadrados da variável Y corrigida pela média é 1.600,9. Assinale a opção que dá a estimativa do aumento esperado no volume de vendas decorrente do aumento de R$ 10.000,00 nos gastos com propaganda, e a soma de quadrados residuais.

• A. R$ 526.000,00 e 373,6
• B. R$ 991.000,00 e 373,6
• C. R$ 526.000,00 e 400,0
• D. R$ 991.000,00 e 400,0
• E. R$ 991.000,00 e 1.600,9

Para a solução das questões de números 38 a 43 utilize o enunciado que segue.

O atributo do tipo contínuo X, observado como um inteiro, numa amostra de tamanho 100 obtida de uma população de 1000 indivíduos, produziu a tabela de freqüências seguinte:

Para a distribuição de freqüências do atributo X sabe-se que

Nessas expressões os i x representam os pontos médios das classes e x a média amostral.

Assinale a opção correta. Considere para sua resposta a fórmula da curtose com base nos momentos centrados e suponha que o valor de curtose encontrado é populacional.

• A.

  A distribuição do atributo X é leptocúrtica.

• B.

  A distribuição do atributo X é platicúrtica.

• C.

  A distribuição do atributo X é indefinida do ponto de vista da intensidade da curtose.

• D.

  A informação dada se presta apenas ao cálculo do coeficiente de assimetria com base nos momentos centrados de X.

• E.

  A distribuição de X é normal.

Para a solução das questões de números 38 a 43 utilize o enunciado que segue.

O atributo do tipo contínuo X, observado como um inteiro, numa amostra de tamanho 100 obtida de uma população de 1000 indivíduos, produziu a tabela de freqüências seguinte:

Assinale a opção que corresponde ao desvio absoluto médio do atributo X.

• A.

  16,0

• B.

  17,0

• C.

  16,6

• D.

  18,1

• E.

  13,0

Num estudo sobre a distribuição do preço de venda de um produto obteve-se, a partir de uma amostra aleatória de 25 revendedores, a tabela de freqüências seguinte:

As quantidades m_i e f_i representam o ponto médio e a freqüência da classe de preços i. Sabendo-se que

assinale a opção que melhor aproxima o desvio padrão amostral.

• A. 0,5 (347/3)^0.5
• B. 6
• C. 0,9 (345/3)^0.5
• D. 28,91
• E. 8

Suponha que o tempo que a Receita Federal leva no processo de devolução do imposto pago a mais tenha distribuição normal com média de 12 semanas e desvio-padrão de 3 semanas. As-sinale a opção que estima a proporção de contribuintes que recebem a devolução em no máximo 6 semanas. A tabela abaixo dá os valo-res de P{0<X<Z} P{0<X<1,56}="0,4406.

• A. 50,00%
• B. 05,56%
• C. 43,32%
• D. 02,28%
• E. 47,72%

Uma lâmpada tem duração em horas (X) que obedece à lei probabilística definida pela função densidade de probabilidades

Assinale a opção que dá o desvio padrão da distribuição de X.

• A.

  32 horas

• B.

  500 horas

• C.

  900 horas

• D.

  800 horas

• E.

  1000 horas

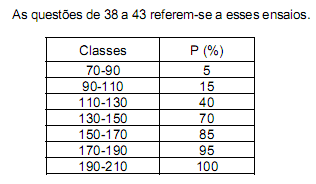
Seja S o desvio padrão do atributo X. Assinale a opção que corresponde à medida de assimetria de X como definida pelo primeiro coeficiente de Pearson.

• A.

  3/S

• B.

  4/S

• C.

  5/S

• D.

  6/S

• E.

  0

Entende-se por curtose de uma distribuição seu grau de achatamento em geral medido em relação à distribuição normal. Uma medida de curtose é dada pelo quociente

onde Q é a metade da distância interquartílica e P₉₀ e P₁₀ representam os percentis de 90% e 10%, respectivamente. Assinale a opção que dá o valor da curtose κ para a distribuição de X.

• A.

  0,263

• B.

  0,250

• C.

  0,300

• D.

  0,242

• E.

  0,000

Um atributo W tem média amostral a ≠ 0 e desvio padrão positivo b ≠ 1. Considere a transformação Z=(W-a)/b. Assinale a opção correta.

• A.

  A média amostral de Z coincide com a de W.

• B.

  O coeficiente de variação amostral de Z é unitário.

• C.

  O coeficiente de variação amostral de Z não está definido.

• D.

  A média de Z é a/b.

• E.

  O coeficiente de variação amostral de W e o de Z coincidem.