Questões de Estatística do ano 2004

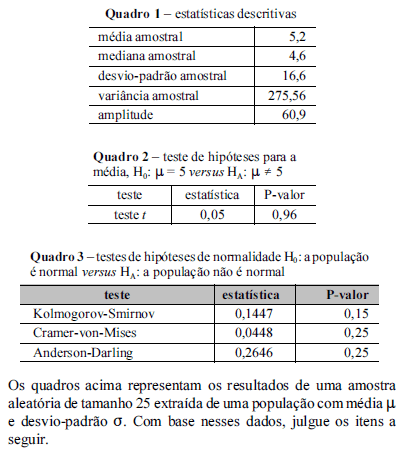
Para um dado ponto x, a maior diferença absoluta observada entre a função de distribuição empírica F(x) e a função de distribuição sob hipótese de normalidade dos dados G(x) é inferior a 0,15.

• C. Certo
• E. Errado

A partir do texto acima, julgue os itens a seguir.

• C. Certo
• E. Errado

Um sinal Z é uma variável aleatória definida por uma soma de variáveis aleatórias independentes X e Y, isto é, Z = X + Y. A variável aleatória X tem distribuição normal com média 10 e desvio-padrão 2, enquanto Y tem distribuição normal com média zero e desvio-padrão 1. Nesse contexto, julgue os itens a seguir.

O valor esperado de Z é igual a 10.

• E. Errado
• C. Certo

Um sinal Z é uma variável aleatória definida por uma soma de variáveis aleatórias independentes X e Y, isto é, Z = X + Y. A variável aleatória X tem distribuição normal com média 10 e desvio-padrão 2, enquanto Y tem distribuição normal com média zero e desvio-padrão 1. Nesse contexto, julgue os itens a seguir.

O desvio-padrão de Z é igual a 3.

• C. Certo
• E. Errado

Um sinal Z é uma variável aleatória definida por uma soma de variáveis aleatórias independentes X e Y, isto é, Z = X + Y. A variável aleatória X tem distribuição normal com média 10 e desvio-padrão 2, enquanto Y tem distribuição normal com média zero e desvio-padrão 1. Nesse contexto, julgue os itens a seguir.

A covariância entre X e Y é inferior a 0,05.

• C. Certo
• E. Errado

Um sinal Z é uma variável aleatória definida por uma soma de variáveis aleatórias independentes X e Y, isto é, Z = X + Y. A variável aleatória X tem distribuição normal com média 10 e desvio-padrão 2, enquanto Y tem distribuição normal com média zero e desvio-padrão 1. Nesse contexto, julgue os itens a seguir.

Z tem distribuição normal.

• C. Certo
• E. Errado

Um sinal Z é uma variável aleatória definida por uma soma de variáveis aleatórias independentes X e Y, isto é, Z = X + Y. A variável aleatória X tem distribuição normal com média 10 e desvio-padrão 2, enquanto Y tem distribuição normal com média zero e desvio-padrão 1. Nesse contexto, julgue os itens a seguir.

A variável aleatóriatem distribuição normal padrão.

• C. Certo
• E. Errado

De acordo com a situação hipotética acima e com a ajuda da tabela da distribuição normal padrão fornecida anteriormente, julgue os itens a seguir.

Dos 100 alunos, 20 tiraram notas iguais ou superiores a 3.

• C. Certo
• E. Errado

Uma revenda de automóveis vende carros montados no Brasil. O proprietário está interessado em estimar o valor médio θ dos gastos extras com opcionais casados com a compra de carros novos. Uma amostra de 16 vendas produziu um valor médio de R$1.062,00 com desvio padrão de R$ 144,00. Assinale a opção que dá os limites de confiança para θ com coeficiente de 98%. A tabela abaixo dá os quantis x , de ordem γ , 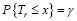 , da distribuição T de Student com r graus de liberdade.

Despreze centavos.

• A.

  [R$ 955,00; R$ 1.168,00]

• B.

  [R$ 968,00; R$ 1.155,00]

• C.

  [R$ 990,00; R$ 1.134,00]

• D.

  [R$ 997,00; R$ 1.124,00]

• E.

  [R$ 938,00; R$ 1.186,00]

Considere o teste da hipótese H : μ =100 contra alternativa A : μ ≠ 100 em uma amostra da normal com média μ e variância σ2. O valor da estatística teste t com distribuição de Student sob a hipótese H : μ =100 é de –1,7864 e sabe-se que P(t≥1,7864)=0,0446.Suponha que a probabilidade de erro do tipo I esteja sendo controlada em 5%. Assinale a resposta correta.

• A.

  Como o valor probabilístico do teste é 0,0446 conclua H :μ = 100.

• B.

  Como o valor probabilístico do teste é 0,0446 conclua A:μ ≠ 100.

• C.

  Como o valor probabilístico do teste é 0,0892 não há evidência para rejeitar H :μ = 100.

• D.

  Como o valor probabilístico do teste é 0,0223 conclua A:μ ≠ 100.

• E.

  Não se pode tirar nenhuma conclusão pois, o tamanho da amostra, a média amostral e o desvio padrão amostral não foram dados.