Questões de Estatística do ano 2004

Para os itens a seguir, utilize, se necessário, as tabelas abaixo para calcular os valores das probabilidades da distribuição normal padrão e valores de 

Uma unidade de produção demanda uma quantidade aleatória D (em kg/dia) de um componente químico. A unidade de produção mantém um estoque X desse componente em kg/dia. Sabe-se que as duas variáveis aleatórias são normais. A distribuição conjunta (D, X) está representada pela tabela abaixo.

Com base na situação hipotética acima, julgue os itens a seguir.

A probabilidade condicional é nula.

• C. Certo
• E. Errado

Uma empresa desenvolveu um sistema de coleta e transmissão de dados. Devido a reclamações por parte de um dos seus clientes, o departamento de controle de qualidade (DCQ) fez um estudo, considerando um período de 300 dias, e identificou os problemas possíveis e a freqüência esperada (em dias) de cada um deles, conforme a tabela abaixo.

Com base nessa situação hipotética, julgue os itens que se seguem.

Para certo dia, a probabilidade de os dados coletados serem corretamente armazenados no computador local é superior a 0,65.

• C. Certo
• E. Errado

Suponha que o motor de um avião em vôo falhe, independentemente dos outros motores, com probabilidade 1-p, sendo p um número entre zero e um. O avião é capaz de fazer um vôo seguro se pelo menos a metade de seus motores estiverem funcionando propriamente. Assinale a opção que corresponde aos valores de p para os quais voar num avião com 4 motores é mais seguro do que voar num bimotor.

• A.

  p=0,500

• B.

  p=0,200

• C.

  p deve estar entre 0,500 e 0,655

• D.

  p deve ser menor do que 0,200

• E.

  p deve ser maior que 2/3

Num estudo do consumo de combustível para uma determinada marca de automóvel, supõe-se que a distribuição do consumo é aproximadamente normal com média desconhecida μ Km/l e desvio padrão de 3 Km/l. Uma amostra de 36 veículos produziu a média de consumo de 16 Km/l. Deseja-se testar a hipótese H: μ =15 contra a alternativa A:μ >15 . Considerando os valores da função de distribuição da normal padrão dados abaixo, assinale a opção que dá o valor probabilístico (p-valor) do teste que toma por base a estatística , sendo a média amostral.

• A.

  0,500

• B.

  0,977

• C.

  0,050

• D.

  0,023

• E.

  0,010

Sejam  variáveis aleatórias independentes com distribuição exponencial com média 0,5. Usando o Teorema Central do Limite e a tabela da função de distribuição da normal padrão dada na questão 49, assinale a opção que corresponde à probabilidade de que

• A.

  0,500

• B.

  0,014

• C.

  0,975

• D.

  0,977

• E.

  0,025

Suponha que, de uma grande população, n pessoas serão selecionadas ao acaso. Da amostra, contar-se-á o número k de pessoas (k < n) que possuem uma determinada doença. De acordo com estudos médicos anteriores, acredita-se que 10% dos indivíduos dessa população têm essa doença. Considere X a variável aleatória que representa o número de pessoas observadas na amostra que possuem a doença.

A partir do texto acima, julgue os itens a seguir.

Se, de fato, 10% dos indivíduos dessa população têm a doença, então a média de X é igual a 0,1n.

• C. Certo
• E. Errado

Suponha que, de uma grande população, n pessoas serão selecionadas ao acaso. Da amostra, contar-se-á o número k de pessoas (k < n) que possuem uma determinada doença. De acordo com estudos médicos anteriores, acredita-se que 10% dos indivíduos dessa população têm essa doença. Considere X a variável aleatória que representa o número de pessoas observadas na amostra que possuem a doença.

A partir do texto acima, julgue os itens a seguir.

Se, de fato, 10% dos indivíduos dessa população têm a doença, então, em uma amostra de 5 pessoas, a probabilidade de que pelo menos uma pessoa tenha a doença é inferior a 0,45.

• C. Certo
• E. Errado

Durante uma aula o professor pediu a seus alunos que pegassem, ao acaso, uma bolinha de uma urna que continha várias bolinhas coloridas, anotassem a cor e a devolvessem à urna. Pediu ainda que repetissem várias vezes esse procedimento e que, ao final, calculassem o porcentual de vezes em que foi sorteada uma bolinha de cor preta. Estes foram os resultados:

Com base nos resultados dessa tabela, os alunos concluíram que a probabilidade de ser sorteada uma bolinha preta da urna era igual a 32%. Essa conclusão, tirada pelos alunos, está:

• A.

  errada, porque não é correto considerar o resultado de um experimento aleatório, mesmo que repetido várias vezes, como valor exato da probabilidade de ocorrência de determinado evento deste experimento.

• B.

  correta, porque a probabilidade é, de fato, o resultado da tabulação experimental da ocorrência de alguma característica que desejamos observar.

• C.

  correta, porque se em 32% das vezes uma bolinha preta foi sorteada, podemos concluir que se houverem 100 bolinhas na caixa, 32 delas serão pretas.

• D.

  errada, porque não sendo conhecido o número de repetições do sorteio, não é possível determinar se a probabilidade de ocorrer bolinha preta é mesmo 32%.

• E.

  errada, porque o cálculo da probabilidade em questão não depende do número de bolinhas pretas existentes na urna, e sim do número de vezes em que o sorteio é realizado.

Para resolver às questões de números 51 a 53 considere o enunciado abaixo.

A proporção de vezes em que o valor de X2 supera o de X1 é

• a.

  0,4

• b.

  0,5

• c.

  0,6

• d.

  0,7

• e.

  0,8

Em relação à situação hipotética apresentada no texto, julgue os itens a seguir.

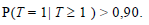
• C. Certo
• E. Errado