Questões de Estatística do ano 2007

Numa população, 10% das pessoas já tiveram hepatite. Se uma amostra aleatória simples de tamanho 400 for observada, a probabilidade de que ao menos 50 já tenham tido hepatite é aproximadamente de:

• A.

  0,015;

• B.

  0,021;

• C.

  0,032;

• D.

  0,057;

• E.

  0,063.

Uma variável aleatória X tem distribuição binomial com parâmetros n = 25 e p = 1/2. Se usarmos aproximação normal à binomial para calcularmos, com correção de continuidade, P[ 10 < X < 15 ] , obteremos aproximadamente:

• A.

  0,444;

• B.

  0,488;

• C.

  0,532;

• D.

  0,576;

• E.

  0,598.

Uma população é composta por três elementos: 0, 0 e 1. Uma amostra aleatória simples de tamanho n = 2 será observada. A probabilidade de que a média amostral seja maior ou igual a 0,5 é igual a:

• A.

  1/3;

• B.

  1/2;

• C.

  2/3;

• D.

  4/5;

• E.

  5/9.

Para que possamos garantir, com 99% de probabilidade, que o valor da média amostral - obtida a partir de uma amostra aleatória simples - não difira do da média populacional por mais de 5% do desvio padrão populacional, o tamanho da amostra deve ser, aproximadamente, no mínimo de:

• A.

  1.621;

• B.

  2.048;

• C.

  2.662;

• D.

  2.956;

• E.

  3.354.

Uma população é constituída por 50 elementos, dos quais 20 têm uma certa característica. Se 8 elementos dessa população forem selecionados ao acaso, sem reposição, então a variância do número de elementos que têm aquela característica na amostra é aproximadamente igual a:

• A.

  0,95;

• B.

  1,65;

• C.

  2,05;

• D.

  2,55;

• E.

  2,85.

Uma urna contém quatro bolas brancas, duas verdes e duas azuis. Três bolas serão sorteadas ao acaso, sem reposição. A probabilidade condicional de que a terceira bola seja branca dado que a primeira sorteada é verde é igual a:

• A.

  1/9

• B.

  2/7

• C.

  1/3

• D.

  2/5

• E.

  3/4

A função geradora de momentos de uma variável aleatória X é dada por:

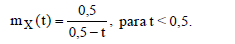
O valor de E[X²] é:

• A.

  0

• B.

  0,5

• C.

  1

• D.

  2

• E.

  8

Se X₁, X₂, ..., X_n é uma amostra aleatória simples de tamanho n de uma distribuição Poisson com parâmetro l então a distribuição de 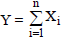 é Poisson com parâmetro:

• A.

  l;

• B.

  n;

• C.

  nl;

• D.

  2n;

• E.

  n/2.

Considere X₁, X₂, ... X_n amostra aleatória simples de uma distribuição exponencial com parâmetro l dada por

f (x) = λe^−λx , x > 0 , l > 0.

O estimador de máxima verossimilhança de l é:

• A.
• B.
• C.
• D.
• E.

Suponha que indivíduos possam ser classificados em cinco categorias: A, B, C, D e E, todas com probabilidade 20%. Se dez indivíduos forem observados de modo independente, a probabilidade de que dois sejam classificados como A, três como B, dois como C, dois como D e um como E é aproximadamente igual a:

• A.

  0,0001;

• B.

  0,008;

• C.

  0,012;

• D.

  0,22;

• E.

  0,36.