Questões de Estatística do ano 2010

O tempo, em horas, que uma empresa leva para localizar e reparar uma avaria elétrica, em um determinado setor, é uma variável aleatória X, cuja função densidade é dada por:

• A.

  1/3

• B.

  2/5

• C.

  1/2

• D.

  2/3

• E.

  3/4

Uma empresa possui um serviço de atendimento ao consumidor (SAC). Diariamente, um atendente registra, em uma folha de papel, as chamadas recebidas. Cada folha de registro do atendente do SAC permite o registro de até 20 chamadas. O atendente efetua os registros de forma sequencial, anotando, para cada chamada, se houve reclamação. De acordo com os dados históricos, sabe-se que, a cada 20 chamadas, a probabilidade de se registrar exatamente uma reclamação é constante e igual a 0,05. Sabe-se também que o número médio diário de reclamações registradas pelo SAC é igual a 1.

Com base nessas informações e considerando 2,71 como valor aproximado para o número e, base do logaritmo natural, julgue os itens de 83 a 86.

Suponha que o número de reclamações registradas pelo SAC, X(t), em um intervalo de tempo t, siga um processo de Poisson e que X(1) represente o número diário de reclamações registradas. Nessa situação, é correto afirmar que a variância de X(t) cresce linearmente com t.

• C. Certo
• E. Errado

Uma empresa possui um serviço de atendimento ao consumidor (SAC). Diariamente, um atendente registra, em uma folha de papel, as chamadas recebidas. Cada folha de registro do atendente do SAC permite o registro de até 20 chamadas. O atendente efetua os registros de forma sequencial, anotando, para cada chamada, se houve reclamação. De acordo com os dados históricos, sabe-se que, a cada 20 chamadas, a probabilidade de se registrar exatamente uma reclamação é constante e igual a 0,05. Sabe-se também que o número médio diário de reclamações registradas pelo SAC é igual a 1.

Com base nessas informações e considerando 2,71 como valor aproximado para o número e, base do logaritmo natural, julgue os itens de 83 a 86.

Considere que o número de reclamações registradas pelo SAC, X(t), em um intervalo de tempo t, siga um processo de Poisson e que X(5) represente o número de reclamações registradas em um intervalo de 5 dias úteis. Nesse caso, a probabilidade de não haver reclamações registradas em um intervalo de 5 dias úteis é igual a e^-5

• C. Certo
• E. Errado

Com base nessas informações, julgue os itens seguintes.

• C. Certo
• E. Errado

Com base nessas informações, julgue os itens seguintes.

• C. Certo
• E. Errado

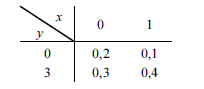
Considerando que tabela acima apresente a distribuição conjunta das variáveis aleatórias X e Y, julgue os itens que se seguem.

A esperança condicional E(X | Y = 3) é inferior a 0,45.

• C. Certo
• E. Errado

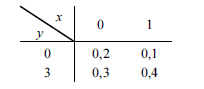
Considerando que tabela acima apresente a distribuição conjunta das variáveis aleatórias X e Y, julgue os itens que se seguem.

O desvio padrão de X é igual a 0,5.

• C. Certo
• E. Errado

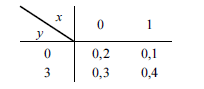
Considerando que tabela acima apresente a distribuição conjunta das variáveis aleatórias X e Y, julgue os itens que se seguem.

O valor esperado de X é superior a 0,6.

• C. Certo
• E. Errado

Uma corporação é formada por uma empresa de mineração e uma empresa petrolífera. Considere que X represente as despesas mensais, em milhões de reais, com a recuperação de danos ao meio ambiente causados pela empresa de mineração e que Y represente as despesas mensais, também em milhões de reais, com a recuperação de danos ambientais causados pela empresa petrolífera. Considere, ainda, que X e Y sejam variáveis aleatórias cuja distribuição conjunta é dada por

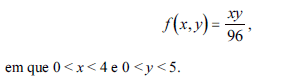
Com base nessas informações, julgue os próximos itens.

O valor esperado de Y é superior a 2,5 milhões de reais.

• C. Certo
• E. Errado

Uma corporação é formada por uma empresa de mineração e uma empresa petrolífera. Considere que X represente as despesas mensais, em milhões de reais, com a recuperação de danos ao meio ambiente causados pela empresa de mineração e que Y represente as despesas mensais, também em milhões de reais, com a recuperação de danos ambientais causados pela empresa petrolífera. Considere, ainda, que X e Y sejam variáveis aleatórias cuja distribuição conjunta é dada por

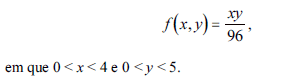
Com base nessas informações, julgue os próximos itens.

A equação matemática que descreve o valor esperado de X em função de Y depende unicamente de y.

• C. Certo
• E. Errado